Erläutern Sie folgendes Gleichungssystem

Question

Aufgabe: Lösen Sie das folgende Gleichungssystem. Es liefert die Koeffizienten eines
Sprungs des Monstertrucks.

Erläutern Sie, welche Eigenschaften des Graphen in der jeweiligen Gleichung beschrieben wird und beschreiben Sie deren Bedeutung im Sachzusammenhang.

c) Für eine „sanfte“ Landung des Trucks ist es wichtig, dass die Rampe die richtige
Steigung besitzt. Begründen Sie, dass die Gleichung 22a + b =-0,2 dies sicher
stellt.

Comments

Vom Duplikat:

Titel: Monstertruck- mit Skizze

Stichworte: lineare-gleichungssysteme

Aufgabe:

Text erkannt:

\( 5 K 122 E x_{1} \)
\( \frac{1}{0} \frac{\sqrt{1}}{11} \)

Lösen Sie das folgende Gleichungssystem. Es liefert die Koeffizienten eines
Sprungs des Monstertrucks.

Ein Monstertruck führt einen Sprung über eine Rampe vor. Seine Flugbahn ist bekanntermaßen eine Parabel mit der Gleichung f(x) = ax2 + bx + c. Skizze verdeutlicht grafisch die Verhältnisse

  a+b+c=1,5

  121a+11b+c=1,5

   2a+b=2

Erläutern Sie, welche Eigenschaften des Graphen in der jeweiligen Gleichung beschrieben wird und beschreiben Sie deren Bedeutung im Sachzusammenhang.

c) Für eine „sanfte“ Landung des Trucks ist es wichtig, dass die Rampe die richtige
Steigung besitzt. Begründen Sie, dass die Gleichung 22a + b =-0,2 dies sicher
stellt.

Answer 1

Eine Parabel hat die Gleichung

f(x) = ax² + bx + c
f'(x) = 2ax + b

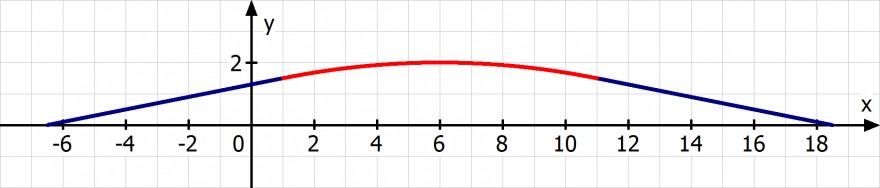
Die 2 Bedingungen die man der Skizze entnimmt sind

f(1)=1.5 --> a + b + c = 1,5
f(11)=1.5 --> 121a + 11b + c = 1,5

Nun hat man noch eine weitere Gleichung 22·a + b = -0.2 gegeben.

22·a + b = -0.2 → f'(11) = -0.2 → Das die Steigung an der Stelle 11 -1/5 ist kann man hier der schlechten Skizze nicht wirklich entnehmen. Da wir aufgrund der Symmetrie der Parabel an der Stelle 1 die Steigung 1/5 haben müssen wäre dieses eher der Skizze zu entnehmen.

Man hat also das folgende LGS

a + b + c = 1,5
121a + 11b + c = 1,5
22·a + b = -0.2

II - I ; III

120a + 10b = 0
22·a + b = -0.2

10·II - I

100·a = -2 → a = -0.02

22·(-0.02) + b = -0.2 --> b = 0.24

(-0.02) + (0.24) + c = 1.5 --> c = 1.28

Die Funktion könnte also lauten

f(x) = -0.02·x² + 0.24·x + 1.28

Damit müsste die Skizze wie folgt aussehen

Comments

Ich verstehe es echt nicht. Welche Eigenschaften des Graphen f(x) = ax²+bx + c werden denn in den drei Gleichungen genannt?

Ich hätte jetzt gesagt, dass a für die Streckung steht, aber a ist immer positiv und die Parabel ist sozusagen nach unten geöffnet??? Irgendwie komme ich bei b mit der Verschiebung auf x-Achse auch nicht weiter. Bitte um Hilfe, da ich eine so ähnliche Aufgabe lösen muss.

---

Ich habe meine Antwort mal zusammengefasst und ergänzt.

---

Danke, aber welche Eigenschaftwn werden denn nun in der jeweiligen Gleichung beschrieben?

---

f(1) = 1.5 → Der Funktionswert an der Stelle 1 ist 1.5

f(11) = 1.5 → Der Funktionswert an der Stelle 11 ist 1.5

f'(11) = -0.2 → Die Steigung an der Stelle 11 ist -0.2 = -1/5