Ich habe folgende lineare Abbildung gegeben:
\( \Phi: \mathbb{R}^{3} \rightarrow \mathbb{R}^{2}, \quad\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right) \mapsto\left(\begin{array}{c}{x-2 y+z} \\ {-4 x+2 y-z}\end{array}\right) \).
Nun möchte eine Basis C des Bildraums \( \mathbb{R}^{2}\) finden, sodass die Abbildungsmatrix bezüglich B und C die Gestalt
\( M_{\mathscr{C}}^{\mathscr{B}}(\Phi)=\left(\begin{array}{lll}{0} & {1} & {0} \\ {0} & {0} & {1}\end{array}\right) \)
besitzt.
Hierbei beschreibt B die Basis dreier Vektoren (des \( \mathbb{R}^{3}\)), welche in einer vorherigen Aufgabe berechnet wurde. B ist folgende:
\( B_{\varepsilon_{2}}^{\varepsilon_{3}}(\Phi)=\left(\begin{array}{ccc}{1} & {-2} & {1} \\ {-4} & {2} & {-1}\end{array}\right) \)
Problem/Ansatz:
Leider weiß ich nicht wie ich dies bestimmen kann. Ein Beispiel würde mir sehr weiterhelfen. Mein Ansatz war folgender:
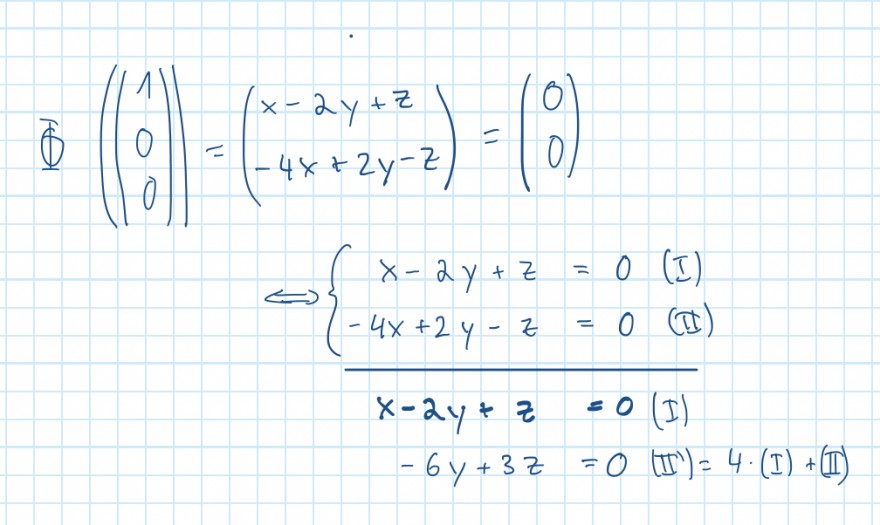
Also im Prinzip so wie ich in der vorherigen Aufgabe die Abbildungsmatrix bestimmt habe, nur nich mit Konkreten Basis-Werten, sondern mit Koordinaten, welche ich mit den jeweiligen Werten aus der Abbildungsmatrix M entnommen habe. Geht aber nicht, da 3 Variablen in 2 "Zeilen" des LGS..
Vielen Dank für jede Antwort!
