Koordinatenvektoren und Abbildungsmatrix bestimmen

Question

Aufgabe:

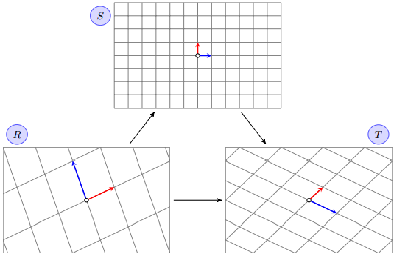
Es seien die drei Basen R = {r1, r2}, S = {s1, s2} (Standardbasis) und T = {t1, t2} des Vektorraums
V = R2 gegeben:
r1 = (−1, 3), r2 = (2, 1); s1 = (1, 0), s2 = (0, 1); t1 = (2, −1), t2 = (1, 1).
Für v ∈ V bezeichnen wir mit vR := γR(v) den Koordinatenvektor von v bzgl. der Basis R (und
dementsprechend vS, vT für die Koordinatenvektoren bzgl. der beiden anderen Basen).
a) Bestimmen Sie für v = (x, y) ∈ R2 die beiden Koordinatenvektoren vR und vT (in Abhängigkeit
von x, y ∈ R).
b) Bestimmen Sie diejenige Matrix M ∈ R2×2 , für die M · vR = vT für alle Vektoren v ∈ V gilt.

Text erkannt:

8
\( 1+2 \pi \)
\( \sqrt[-1]{\frac{1}{1} \cdot \sqrt{1}}{1} \)

wie kann man hier die Koordinatenvektoren und Abbildungsmatrix bestimmen.

Ich bin mir irgendwie total unschlüssig, wie ich an die Sache heran gehen soll. Wäre cool, wenn mir jemand helfen könnte :)

Answer 1

Aloha :)

Die drei Basen sind: \(R=\left(\begin{array}{c}-1 & 2\\3 & 1\end{array}\right)\quad;\quad S=\left(\begin{array}{c}1 & 0\\0 & 1\end{array}\right)\quad;\quad T=\left(\begin{array}{c}2 & 1\\-1 & 1\end{array}\right)\)

Die Komponenten der Basen sind alle bezüglich der Standardbasis \(S\) angegeben. Wenn man also einen Vektor \(\vec v_R\) mit Koordinaten bezüglich der Basis \(R\) von rechts an die Matrix \(R\) multipliziert, erhält man die Komponenten des Vektors \(\vec v\) bezüglich der Standardbasis. Analog gilt dasselbe für die Basis \(T\). Formal heißt das:

$$\vec v={_Sid_R}\cdot\vec v_R=R\cdot\vec v_R\quad;\quad \vec v={_Sid_T}\cdot\vec v_T=T\cdot\vec v_T$$Wenn man die linke Gleichung von links mit \(R^{-1}\) und die rechte von links mit \(T^{-1}\) multipliziert, erhalten wir die in Teil (a) gesuchten Transformationsregeln:

$$\vec v_R={_Rid_S}\cdot\vec v=R^{-1}\cdot\vec v=\left(\begin{array}{c}-1 & 2\\3 & 1\end{array}\right)^{-1}\left(\begin{array}{c}x\\y\end{array}\right)=\frac{1}{7}\left(\begin{array}{c}-1 & 2\\3 & 1\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)$$$$\vec v_T={_Tid_S}\cdot\vec v=T^{-1}\cdot\vec v=\left(\begin{array}{c}2 & 1\\-1 & 1\end{array}\right)^{-1}\left(\begin{array}{c}x\\y\end{array}\right)=\frac{1}{3}\left(\begin{array}{c}1 & -1\\1 & 2\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)$$

In Teil (b) soll die Matrix \(M\) bestimmt werden, die die Komponenten des Vektors \(\vec v_R\) bezüglich der Basis \(R\) in die Komponenten des Vektors \(\vec v_T\) bezüglich der Basis \(T\) transformiert. Um von \(R\to T\) zu transformieren, kann man zuerst von \(R\to S\) und dann von \(S\to T\) transformieren:

$$M={_T}id_R={_T}id_S\cdot {_S}id_R=T^{-1}R=\frac{1}{3}\left(\begin{array}{c}1 & -1\\1 & 2\end{array}\right)\left(\begin{array}{c}-1 & 2\\3 & 1\end{array}\right)=\frac{1}{3}\left(\begin{array}{c} -4 & 1\\ 5 & 4\end{array}\right)$$

Answer 2

Hallo

 einfach die Linearkombination der einen Basisvektoren durch die anderen bestimmen. etwa

r1=-1*s1+3*s2

entsprechend r1 durch t1 und t2 kombinieren usw.

Gruß lul