Vom Duplikat:
Titel: Fehler beim Ableiten von ln mit Wurzel f(x) = ln( 3.Wurzel aus (x^2-1)/(x^2+1)
Stichworte: ableitung,logarithmengesetze,logarithmus,brüche
Aufgabe: Falsches Bild

Text erkannt:
\( 02 . f(x)=5 * \ln \sqrt{\frac{x+1}{x-1}}-8 \)
\( f^{\prime}(x)=\frac{-5}{x^{2}-1} \)
Links ist die Funktion zu sehen, die abgeleitet werden soll. Rechts ist die Ableitung der Funktion zu sehen.
Problem/Ansatz: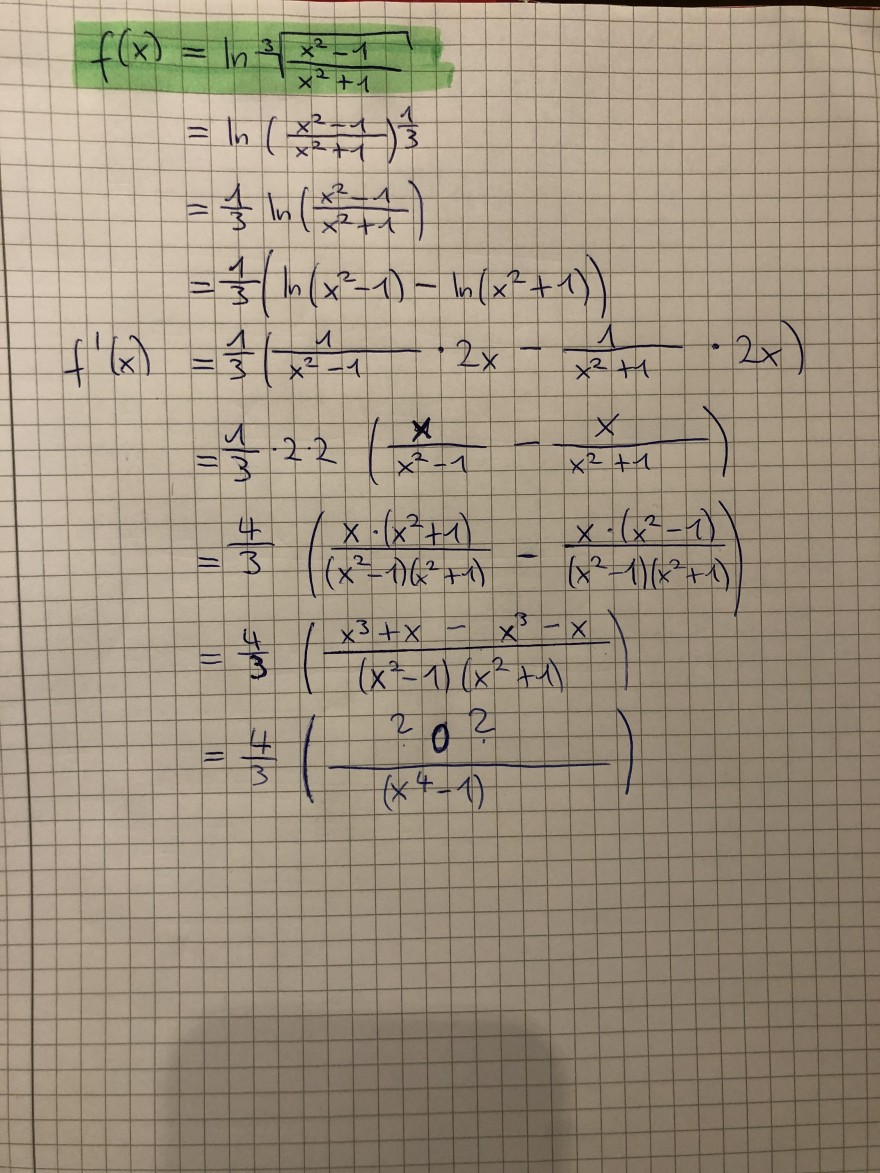
Text erkannt:
\( \begin{aligned} f(x) &=\ln \sqrt[3]{\frac{x^{2}-1}{x^{2}+1}} \\ &=\ln \left(\frac{x^{2}-1}{x^{2}+1}\right)^{\frac{1}{3}} \\ &=\frac{1}{3} \ln \left(\frac{x^{2}-1}{x^{2}+1}\right)^{\frac{1}{3}} \\ &=\frac{1}{3}\left(\ln \left(x^{2}-1\right)-\ln \left(x^{2}+1\right)\right) \\ &=\frac{1}{3}\left(\frac{1}{x^{2}-1} \cdot 2 x-\frac{x}{x^{2}+1}\right) \\ f^{\prime}(x) &=\frac{4}{3}\left(\frac{x^{2}+x-x^{3}-x}{\left(x^{2}-1\right)\left(x^{2}+1\right)}\right) \\ &=\frac{4}{3}\left(\frac{20^{2}}{\left(x^{4}-1\right)}\right) \end{aligned} \)
Mein Ansatz ist Letzterer. Irgendwo muss mir ein Fehler unterlaufen sein. Ich habe extra jeden Schritt sehr kleinteilig aufgeschrieben, damit alles nachzuvollziehen ist. Die richtige Lösung ist rechts neben der Aufgabe zu finden.