Globales Maximum unter Nebenbedingungen

Question

Aufgabe:

Sei f: R^2 -> R durch f(x,y) := e^(x^2+y^2) und M ⊂ R^2 gegeben durch

M:= {(x,y)^T ∈ R^2 : 0 ≤ y ≤ 1, y ≤ x ≤ y+1

Geben Sie den natürlichen Logarithmus des maximalen Funktionswerts der Einschränkung von f auf M an

Problem/Ansatz:

Kann mir jemand weiterhelfen ich bin überfordert, danke!

Answer 1

Jeder Kreis um den Ursprung hat die Gleichung x²+y²=r². Für alle Punkte auf einem Kreis um den Ursprung ist also der Wert von x²+y² gleich groß.

Wie groß x²+y² werden kann, hängt also einzig und allein vom Radius des verwendeten Kreises ab.

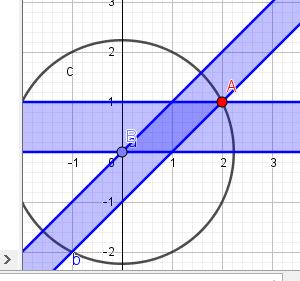
e^x²+y² soll maximal werden.  Es wird maximal, wenn x²+y² maximal wird. Dafür muss es einen möglichst großen Kreis geben, von dem wenigstens ein Punkt (x,y) noch in dem durch die Nebenbedingungen begrenzten Gebiet liegt.

PS: Kann natürlich sein, dass die wollen, dass du hier mit Lagrange draufhaust.

Comments

sorry dass ich nochmal so doof frage aber die Antwort lautet dann 2 richtig?

---

Falsch. Der abgebildete Kreis hat einen Radius, der größer als 2 ist. Damit ist x²+y²=r² sogar größer als 4.

---

4,4 dann oder?

---

Bist du eventuell in der Lage, für die Koordinaten des Punktes (x,y)=(2,1) den Term x²+y² auszurechnen?

---

wären ja 5 aber es kommt eine kommazahl raus

---

aber es kommt eine kommazahl raus

Wer behauptet das?

Answer 2

Aloha :)

Bist du sicher, dass die Aufgabenstellung so richtig ist? Da muss man ja überhaupt nichts rechnen...

Die \(e\)-Funktion ist maximal, wenn ihr Exponent \(x^2+y^2\) maximal ist. Dieser maximale Exponent soll auch als Ergebnis angegeben werden. Er ist gleich dem Quadrat des Abstandes vom Ursprung zum Punkt \((x|y)\).

Für den Punkt \((x|y)\) gibt es folgende Randbedingungen: $$0\le y\le 1\quad;\quad y\le x\le y+1$$Wenn man \(y\) festhält, beschreibt \(x\) eine horizontale Strecke von \(y\) bis \(y+1\). Da \(y\) von \(0\) bis \(1\) läuft, entsteht als Fläche ein Parallelogramm. Der vom Ursprung am weitesten entfernte Punkt ist die rechte obere Ecke \((2|1)\).

Das maximale Quadrat des Abstandes ist daher \(x^2+y^2=5\).