Harmonische Schwingung berechnen: Phasenfreie Form und Zeiger

Question

Aufgabe:

Gegeben ist die harmonische Schwingung in der phasenwinkelfreien Form

x(t)=2⋅3–√⋅sin(4⋅t)+2⋅cos(4⋅t)

Problem/Ansatz:

Geben Sie diese Schwingung in der Form x(t)=A⋅cos(ωt+φ) an.
Geben Sie zusätzlich den Zeiger der Schwingung an.


Mein Ansatz:
A⋅cos(ωt+φ) = 2*√3 *sin(4*t) + 2*cos(4*t), da es gleich C₁ cos(ωt) +C₂ sin(ωt)


Danach weiß ich nicht weiter. Ich was auch nicht, was man mit dem Zeiger so meint.

Answer 1

Hallo

$$a*sin(x)+b*cos(x)=\sqrt{a^2+b^2}*(\frac{a}{\sqrt{a^2+b^2}}*sin(x)+\frac{b}{\sqrt{a^2+b^2}}*cos(x))=\sqrt{a^2+b^2}(sin(x)*sin(φ)+cos(x)*cos(φ))=\sqrt{a^2+b^2}*cos(x-φ)$$

das anwenden, dann tan(φ)=a/b

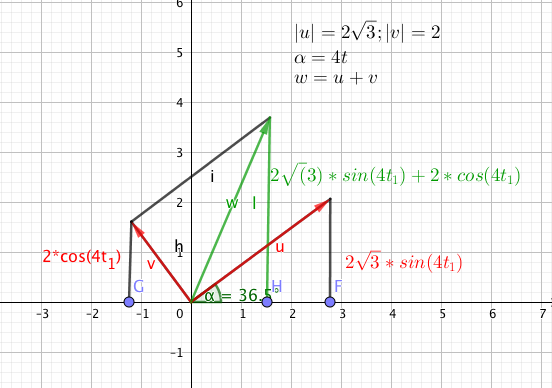
das alles kann man auch an dem Zeigerdiagramm ablesen, das für einen Zeitpunkt gezeichnet ist, aber der grüne Summenzeiger läuft ja ein fach mit t um

Gruß lul