Eine antike Pyramide hat die Ecken A (100|0|0), B(100|100|0), C(0|100|0), D (0|0|0) und die Spitze S (50|50|100). Aus der Seitenfläche BCS ragt als Teil einer Hebevorrichtung senkrecht ein Balken PQ heraus, dessen Mitte T auf einer vertikalen Stütze RT steht. Es gilt P(50 60|80) und Q (50|100|100).
a) Stellen Sie eine Parametergleichung der Ebe- ne E auf, welche B, C und S enthält.
b) Überprüfen Sie, ob der Punkt P tatsächlich auf der Seitenfläche BCS liegt.
c) Weisen Sie nach, dass der Balken PQ senk- recht auf BCS steht. Wie lang ist PQ?
d) Berechnen Sie die Länge der Stütze TR. Stellen Sie dazu die Gleichung der vertikalen Geraden g auf, die den Punkt T enthält. Berechnen Sie dann den Punkt R als Schnittpunkt der Geraden g mit der Fläche BCS.
e) Bestimmen Sie den Mittelpunkt M der Strecke BC. Bestimmen Sie dann den Winkel a = PQM zwischen den Strecken QP und QM.
f) Zeigen Sie, dass die Punkte U(40|40|80) und V (60|40|80) auf zwei Kanten der Pyramide liegen. Begründen Sie, dass das Viereck ADUV ein Trapez ist.
g) An der Position H(70|50 a) liegt ein Schachteingang. Der Schacht führt zur Schatzkammer in der Pyramidenmitte G(50|50|50). Das Sonnenlicht fällt bis in die Schatzkammer G, wenn es in Richtung des Vektors V einfällt. Bestimmen Sie a. 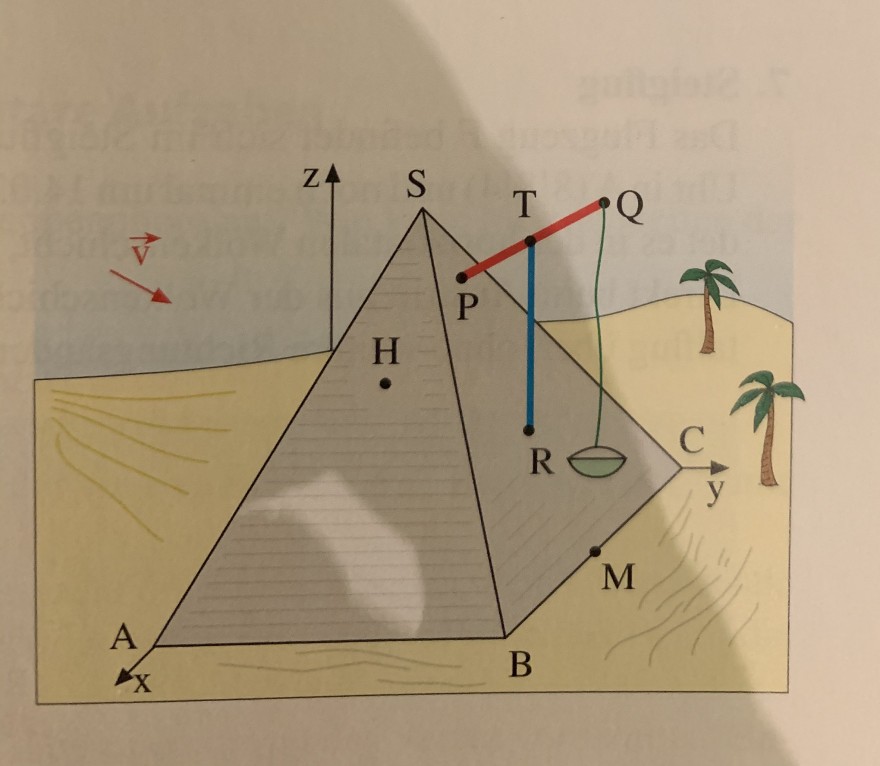
Text erkannt:
157