Bestimmen Sie alle reellen Zahlen {−1,1}, die der Ungleichung genügen

Question

die Aufgabe lautet, dass ich alle reellen Zahlen {−1,1}, die der Ungleichung (|x|−1)/(x^2−1)≥1/2 erfüllen bestimmen soll.

Ich weiß, dass ich eine Fallunterscheidung machen muss, aber ich verstehe das alles nicht so ganz.

Comments

Ich würde gerne wissen ob du {-1,1} exakt so aus der Fragestellung abgeschrieben hast. Eigentlich ist das so wie es dort steht die Menge mit der Zahl -1,1 und damit etwas ganz anderes als (-1, 1) bzw. (-1; 1).

---

Bimmel123, kannst du mal die Notation der Aufgabenstellung

Bestimmen Sie alle reellen Zahlen {−1,1}, die der Ungleichung genügen

auf Richtigkeit überprüfen? Für die so angegebene Menge ist die Ungleichung gar nicht definiert.

---

@mathecoach: Sollten hier nicht auch eckige Klammern vorkommen?

Ich denke alle wissen was gemeint war. Zumindest alle die bisher geantwortet haben. Ich wollte nur nochmal darauf aufmerksam machen, damit der Fragesteller nochmals darüber nachdenkt.

Denn um eine Frage vollständig und richtig beantwortet werden kann wäre es zunächst einmal extrem wichtig das eine Frage vollständig und richtig gestellt wird.

Answer 1

Du musst -1<x<0 und x=0 und 0<x<1 unterscheiden.

Im Nenner wendest du die dritte binomische Formel an.

x^2-1^2=(x-1)(x+1)

Als Ergebnis solltest du alle Zahlen zwischen - 1 und +1 erhalten.

Answer 2

(|x|−1) / (x^2−1) ≥ 1/2
Für x ≥ 0 gilt
( x−1) / [ (x+1)*(x-1) ] ≥ 1/2
Für x ≠ -1 gilt
( x−1) / [ (x+1)*(x-1) ] ≥ 1/2   |  kürzen
1 / ( x + 1 ) ≥ 1/2 |
1 ≥ 1/2 * ( x + 1 ) | * 2
2 ≥ x + 1
x ≤ 1
Zusammen mit der Eingangsvoraussetzung x ≥ 0
 0 ≤ x ≤ 1

Für x ≤ 0 gilt
g ( x ) = (|x|−1) / (x^2−1) - 1/2
g ( x ) = - g ( x )
Die Funktion ist achsensymmetrisch zur y-Achse
Also
-1 ≤ x ≤ 0

Oder führe den Nachweis analog Fall 1

Bei Bedarf nachfragen.

Comments

0 ≤ x ≤ 1

x = 1 erfüllt die Ungleichung sicher nicht.

---

Das verstehe ich auch gerade nicht an der Lösung, wenn ich 1 einsetze kommt doch null raus.

Ich verstehe auch nicht wie (x^{2}−1) zu (x+1)(x-1) wird.

---

Das verstehe ich auch gerade nicht an der Lösung, wenn ich 1 einsetze kommt doch null raus

Nein. Der Term auf der linken Seite hätte die Form 0/0, und das ist nicht 0, sondern es ist NICHT DEFINIERT.

Ich verstehe auch nicht wie (x²−1) zu (x+1)(x-1) wird

Dann multipliziere  (x+1)(x-1) einfach mal aus (Stichwort: dritte binomische Formel).

---

Ok danke für die Antwort!

Ja gut meine zweite Frage war doof ;)

---

In meiner Antwort steckt ein Fehler
(|x|−1) / (x2−1) ≥ 1/2
Für x ≥ 0 gilt
( x−1) / [ (x+1)*(x-1) ] ≥ 1/2
Es muß heißen
Nicht
Für x ≠ -1 gilt
sondern
Für x ≠ 1 gilt
( x−1) / [ (x+1)*(x-1) ] ≥ 1/2  |  kürzen
1 / ( x + 1 ) ≥ 1/2 |
1 ≥ 1/2 * ( x + 1 ) | * 2
2 ≥ x + 1
x ≤ 1
Zusammen mit den Eingangsvoraussetzungen
x ≥ 0 und x ≠ 1 gilt
0 ≤ x < 1

Frag nach bis alle Klarheiten beseitigt sind.

---

Ja danke :) Wäre das bei der zweiten Vorraussetzung dann x ≠ -1

---

(|x|−1) / (x^2−1) ≥ 1/2
3.binomische Formel
(|x|−1) / [ (x−1) * ( x + 1 ) ] ≥ 1/2
2.Fall
Für x < 0 gilt
( x + 1) = 0 ausschließen / Division durch null
x ≠ -1
(|x|−1) = ( -x - 1 )

( -x-1) / [ (x+1)*(x-1) ] ≥ 1/2
(-1) * ( x + 1 ) / [ (x+1)*(x-1) ] ≥ 1/2  | kürzen ( x + 1)
( -1 ) / ( x - 1 ) ≥ 1/2  | x -1 ist stets negativ weil x < 0
Bei einer Multplikation mit x - 1 muß das
Relationzeichen umgedreht werden
-1 < 1/2 * ( x - 1 ) | * 2
- 2 < x -1
-1 < x
x > -1
Zusammen mit der Eingangsvoraussetzung x < 0
und x ≠ -1
-1  < x ≤ 0
Kann sein das noch ein Relationszeichen etwas verbessert werden muß. Habe aber keine Lust mehr.

---

Nachtrag
(|x|−1) / (x^2−1) ≥ 1/2
Etwas anders als Funktion geschrieben
f ( x ) = (|x|−1) / (x^2−1) - 1/2
Die Variable x kommt vor in
| x | und x^2
| +4  | = | -4 |
(+4)^2 = (-4)^2
d.h. das Vorzeichen von x spielt keine Rolle
der Wert von x ist in der Funktion stets positiv
Die Funktion ist also achsensymmetrisch

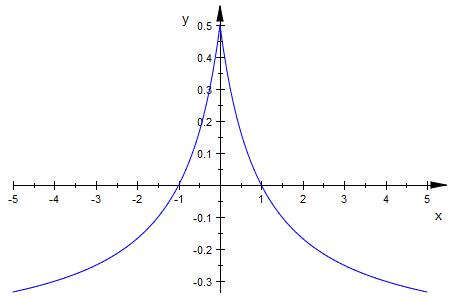
Alles oberhalb der x-Achse gehört zur Lösungsmenge
x von 0 bis 1 und x von -1 bis 0
Die Lösungsmenge ist auch spiegelsymmetrisch

Mit der Erkenntnis kann man sich die doch etwas umfang-
reicheren Berechnungen von Fall 2 sparen.

---

@Bimmel: Du hast immer noch nicht gesagt, welche Klammern da wirklich stehen. Oder?

Ist es nun geschweift { } , rund ( ) oder eckig [ ].