Expotentialfunktion =(1/3)^x

Question

a) skizziere den graphen von f und von f^-1

b) Umkehrungsgleichung rechnerisch bestimmen
c) wo schneidet der graph f die horizontale gerade  y= 5

d) wo schneidet der graph von f^-1  die h. g. y=5

Answer 1

y = (1/3)^x

(1/3)^x = y

x * ln(1/3) = ln(y)

x = ln(y) / ln(1/3)

y = ln(x) / ln(1/3)

Bekommst du Schnittpunkte selber hin? Also

f(x) = 5 und f'(x) = 5 ?

Skizze:

Answer 2

Hi,

a)

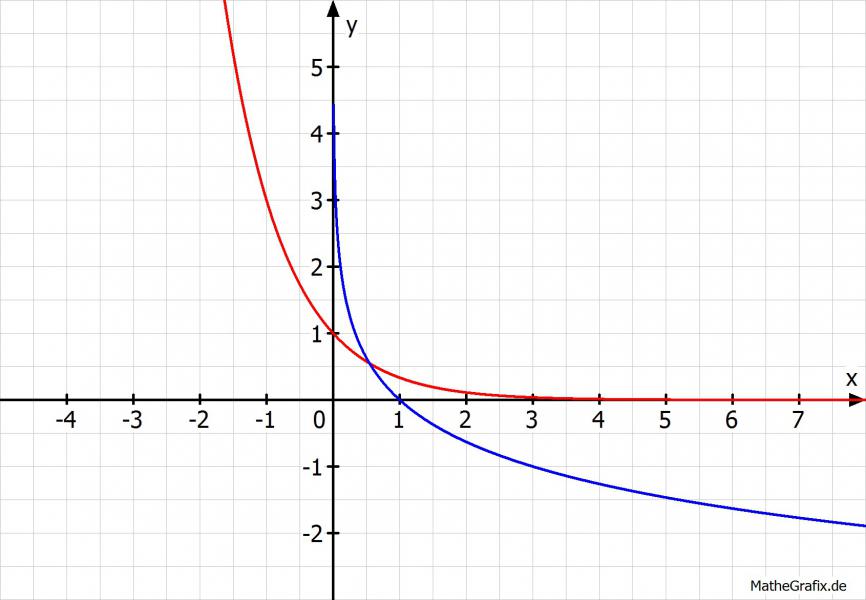
Wobei das Blaue die Umkehrfunktion ist.

 

b)

y = (1/3)^x

Tauschen der Variablen

x = (1/3)^y  |ln

ln(x) = yln(1/3) |:ln(1/3)

ln(x)/ln(1/3) = y   |mit ln(1/3) = ln(1)-ln(3) = -ln(3)

y = -ln(x)/ln(3)

 

c)

y = (1/3)^x = 5

ln(5) = -xln(3)  |:(-ln(3))

x = -ln(5)/ln(3) ≈ -1,465 (siehe auch Schaubild. Das passt)

 

d)

y = -ln(x)/ln(3) = 5

ln(x) = -5ln(3)  |mit -5ln(3) = ln(3^{-5})

x = 3^{-5} ≈ 0,00412

 

Auch das kann man im Schaubild erahnen.

 

Grüße