Aufgabe:
Bestimme die Stammfunktionen der folgenden Funktionen :
1a) f(x)= x^3 + 2
b) f(x)= 4 + 2x-x^2
c) f(x)= x^3 -x
d) f(x)= x^3 + 6x^2
e) f(x)= 1/3 •x^3 -x^2 + 2x
f) f(x) = x^5
g) f(x)= x^4 -12x
h) f(x)= x^5
i) f(x)= x^3 (2+x)
Problem/Ansatz:
Möchte wissen ,ob meine Ergebnisse richtig sind
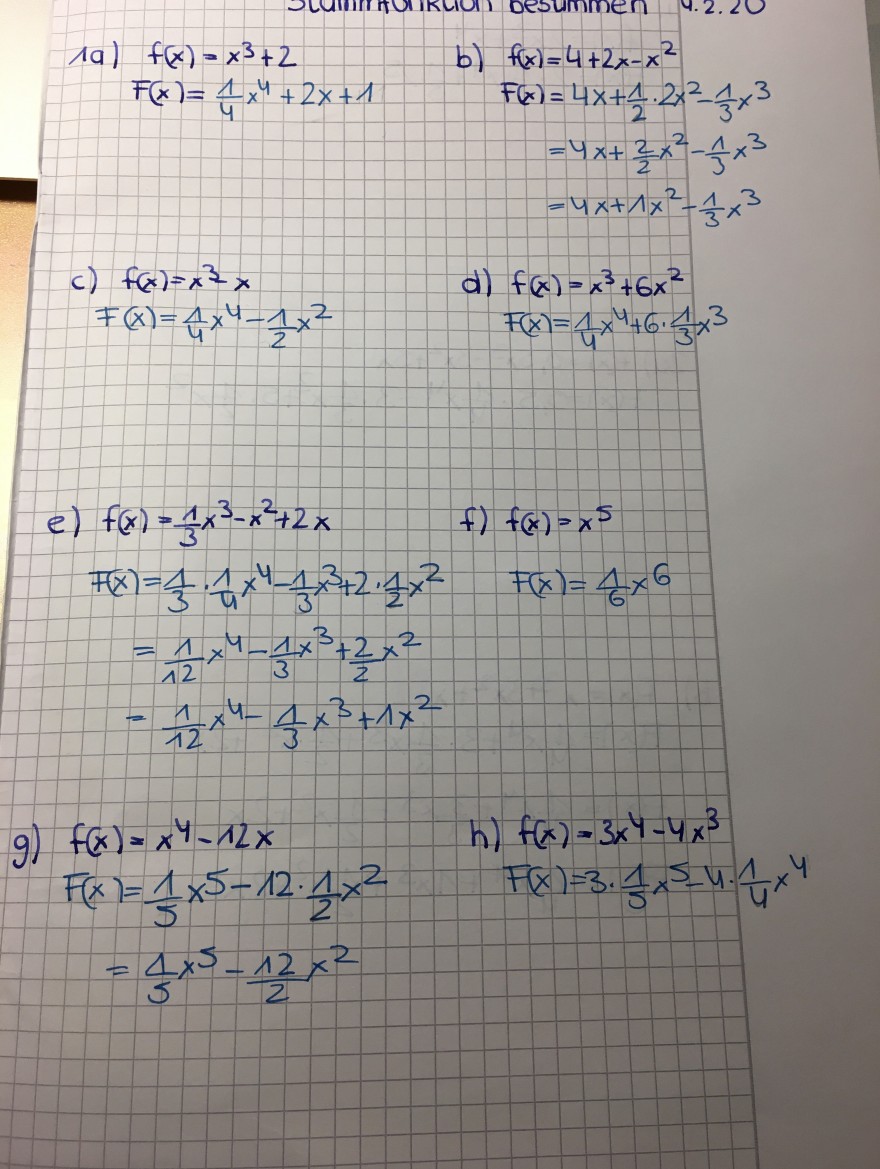
Text erkannt:
1a) \( \quad f(x)=x^{3}+2 \)
b) \( f(x)=4+2 x-x^{2} \)
$$ \begin{array}{rl} {F(x)=\frac{1}{4} x^{4}+2 x+1} & {F(x)=4 x+\frac{1}{2} \cdot 2 x^{2}-\frac{1}{3} x^{3}} \\ {} & {=4 x+\frac{2}{2} x^{2}-\frac{1}{3} x^{3}} \end{array} $$
c) \( f(x)=x^{3}-x \)
a) \( f(x)=x^{3}+6 x^{2} \)
\( F(x)=\frac{1}{4} x^{4}-\frac{1}{2} x^{2} \)
\( F(x)=\frac{1}{4} x^{4}+6 \cdot \frac{1}{3} \)
e) \( f(x)=\frac{1}{3} x^{3}-x^{2}+2 x \)
\( f) f(x)=x^{5} \)
\( F(x)=\frac{1}{3} \cdot \frac{1}{4} x^{4}-\frac{1}{3} x^{3}+2 \cdot \frac{1}{2} x^{2} \)
\( F(x)=\frac{1}{6} x^{6} \)
$$ \begin{array}{l} {=\frac{1}{12} x^{4}-\frac{1}{3} x^{3}+\frac{2}{2} x^{2}} \\ {=\frac{1}{12} x^{4}-\frac{1}{3} x^{3}+1 x^{2}} \end{array} $$
g) \( f(x)=x^{4}-12 x \)
h) \( f(x)=3 x^{4}-4 x^{3} \)
\( F(x)=\frac{1}{5} x^{5}-12 \cdot \frac{1}{2} x^{2} \)
\( F(x)=3 \cdot \frac{1}{5} x^{5}-4 \cdot \frac{1}{4} x^{4} \)
$$ =\frac{1}{5} x^{5}-\frac{12}{2} x^{2} $$

Text erkannt:
i) \( f(x)=x^{3}(2+x) \)
$$ \begin{array}{l} {f(x)=2 x^{3}+x^{4}} \\ {F(x)=2 \cdot \frac{1}{4} x^{4}+\frac{1}{5} x^{5}} \end{array} $$