Sei \( F \subseteq \mathbb{R}^{2} \) ein regelmaliges Viereck. Die Ecken seien im Uhrzeigersinn mit \( 1,2,3,4 \) nummeriert. Die Symmetriegruppe von \( F \) ist per Definition die Diedergruppe \( D_{4} . \) Seien \( D \in D_{4} \) die Drehung um \( 90^{\circ} \) im Uhrzeigersinn, \( S \in D_{4} \) die Spiegelung an der durch 1 und 3 verlaufenden Geraden, und \( T \) die Spiegelung an der durch die Mittelpunkte der Seiten \( 1-2 \) und \( 3-4 \) verlaufenden Geraden.
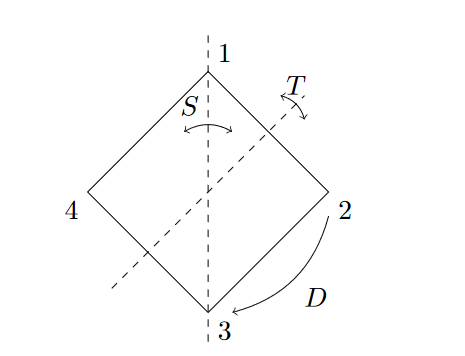
Beschreiben Sie \( D, S, T \) und \( T S \) als Elemente der symmetrischen Gruppe \( S_{4} \).