y = (x + 1) / (2·x + 1)
Eine Umkehrfunktion findest du durch auflösen nach x
y·(2·x + 1) = (x + 1)
2·x·y + y = x + 1
2·x·y - x = 1 - y
x·(2·y - 1) = 1 - y
x = (1 - y) / (2·y - 1)
Zum Schluss wird nur noch x und y vertauscht.
Umkehrfunktion: y = (1 - x) / (2·x - 1)
Jetzt kannst du die Funktionen auch schon mal skizzieren.
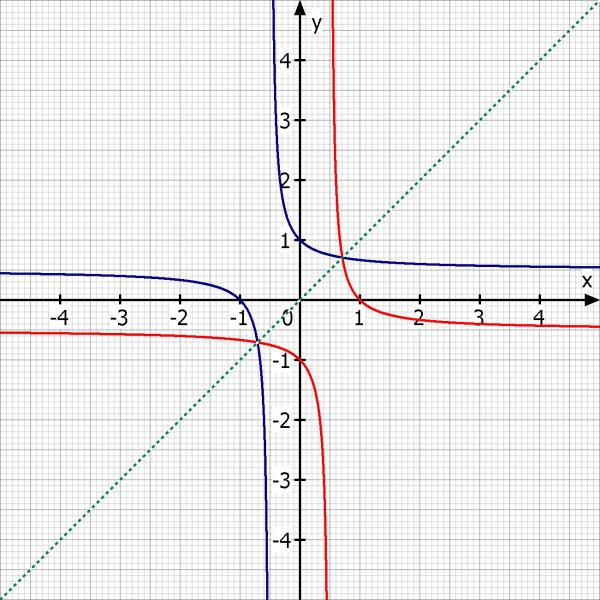
blau ist die Ursprungsfunktion und rot die Umkehrfunktion.
Schau dir den blauen Graphen an. Wo ist der Definitionsbereich und wo der Wertebereich und wie kannst du sie rechnerisch zeigen?