Text erkannt:
\( Z=\frac{X-\mu}{\sigma} \)
Ganz normal mit der Formel Rechnen?
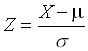
Mein Gedanke ist, dass ich nun die Papierdicke 1/10 und die Standardabweichung 1/50 mit 1000 Multiplizieren muss (wegen 1000 Blatt in Aufgabenstellung a.)?
Z= (X - 20) / 100
wenn das halbwegs richtig sein weiß in dennoch nicht ganz was ich für X einsetzen soll