Verständnisfrage zum Berechnen des Flächeninhaltes eines Zeltdaches

Question

Hallo ich habe eine Verständnisfrage zu dieser Aufgabe.

c) Der Architekt schlägt zwei Dachformen zur Wahl vor: Satteldach oder Zeltdach.

Vergleiche die Größen der Dachflächen beider Dächer miteinander.

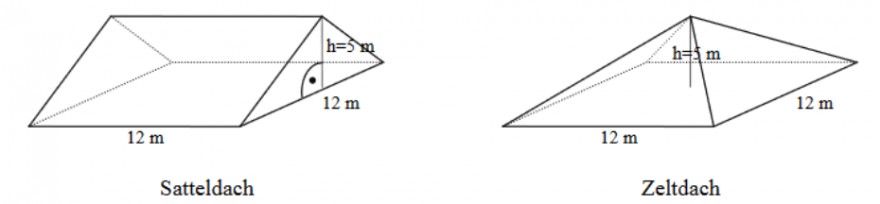
Für das Satteldach ergibt sich A_S= 2*12*b

NR: Satz des Pythagoras führt dazu das ich b erhalte

Dadurch erhalte ich für A_S=187,44

soweit ist mir die Aufgabe auch noch klar.

Jetzt kommt aber das Zeltdach

Hier finde ich folgende Formel für A_Z:  4*\( \frac{12*h}{2} \)

h erhalte ich wieder mit dem Pythagoras was dann wieder 7,8 ist somit komme ich dann ebenfalls auf eine Fläche von 187,44.

Das ist soweit auch okay. Meine Verständnisproblem bezieht sich auf die Formel vom Zeltdach. Da ich Probleme mit der herletiung dieser hatte.

Ich fang einfach mal an.

4= steht für die 4 Dachseiten

12= für die länge der Dachseiten

h= ist die höhe

das war bis dahin auch kein Problem (hoffe meine Erklärung stimmt) was mir nicht klar ist warum muss ich die 12*h durch 2 teilen?

Daher meine Konkrete Frage, warum wird das Ergebnis aus 12*h nochmal halbiert?

Würde mich freuen wenn mir das jemand erklären kann.

Danke

wünsche allen ein schönes Wochenende

Answer 1

Satteldach

A = 2 * 12 * √(6^2 + 5^2) = 187.4 m²

Zeltdach

A = 4 * 1/2 * 12 * √(6^2 + 5^2) = 187.4 m²

Comments

Daher meine Konkrete Frage, warum wird das Ergebnis aus 12*h nochmal halbiert?

Wie berechnet sich noch die Fläche eines Dreiecks?

A = 1/2 * g * h

Answer 2

Ebenfalls mit Pythagoras, wie unten skizziert.

Oder mit Integratonsrechnung würde es auch gehen, ohne Dreiecksflächenformel und ohne Pythagoras:

A_Z =  \( \int\limits_{0}^{5} \) Umfang(\(h\) ) \( = \frac{1}{2}* h \) * 4 * 12  weil der Umfang unten 4*12 ist und oben Null.

Comments

Text erkannt:

Fläche des Satteldaches:
\( A_{S}=2 \cdot 12 \cdot b \)
\( b^{2}=6^{2}+5^{2} \Rightarrow b=\sqrt{61}=7,810 \ldots \)
\( A_{S}=187,44 \ldots \)
Fläche des Zeltdaches:
\( \begin{aligned} A_{z}=4 \cdot \frac{12 \cdot h_{z}}{2} &=24 \cdot h_{z} \\ h^{2} &=6^{2}+5^{2} \Rightarrow h_{z}=\sqrt{61}=7,810 \ldots \end{aligned} \)
\( A_{z}=187,44 \ldots \)
Die Dachflächen haben den gleichen Flächeninhalt.

 Das habe ich als Musterlösung gefunden dazu! Daher ja meine Frage warum wird da durch 2 geteilt

---

Rechne mit den Kathetenlängen 6 m und 5 m direkt die Höhe des Dachdreiecks (die Hypotenuse des grünen Dreiecks) aus:

Die Fläche einer Dachseite ist dann Grundline 12 m mal Höhe dividiert durch 2.

Das Zeltdach hat vier Dachseiten.