Fixkosten und variable Kosten

Question

kann mir bitte jemand mit diesem Beispiel weiterhelfen und mir auch erklären, wie man es löst.

Drei Schüler vergleichen die Kosten für die Nutzung mobilen Internets: Max zahlt 15 € Grundgebühr 704 im Monat und 0,25 € pro 100 MB. Sabine hat keine Grundgebühr, sie bezahlt dafür pro 100 MB 1 €. Klaus zahlt pauschal monatlich 20 €.

1) Beschreibe die jeweilige Kostenfunktion mit einer Tabelle (in 200 MB-Sprüngen) und durch eine Funktionsgleichung und zeichne alle Funktionsgraphen in dasselbe Koordinatensystem (bis 3000 MB = 3 GB). Bei welcher Datenmenge zahlen alle dasselbe?

 2) Sabines Großmutter nutzt höchstens 200 MB im Monat. Für welchen Tarif sollte sie sich entscheiden? Wie viel spart sie im Vergleich zu den beiden anderen Tarifen?

Vielen Dank im Voraus

Comments

Hast Du Probleme mit der Tabelle oder mit den Graphen?

---

Mit beiden, es geht darum, dass ich nicht weiß, wie ich anfangen soll.

Answer 1

Eine Lineare Funktion hat die Form

y = m*x + b

Dabei ist b der y-Achsenabschnitt also z.B. die Grundgebühr und m die Steigung. Also z.B. die Kosten für jeweils 100 MB.  Damit würden die Graphen wie folgt aussehen:

~plot~ 15+0.25*x;x;20;[[0|30|0|30]] ~plot~

Answer 2

1)

Zeichne eine Tabelle mit vier Spalten und 17 Zeilen.

Schreibe in die erste Zeile von links nach rechts: MB, Max, Sabine, Klaus.

Schreibe in die erste Spalte in die freien Felder von oben nach unten: 0, 200, 400, 600 usw. bis 3000.

Schreibe in die vierte Spalte in die freien Felder von oben nach unten überall 20.

Fülle die restlichen Felder aus aufgrund der in der Aufgabenstellung angegebenen Formeln.

Für die Graphen wirst Du etwas in der Art haben wollen:

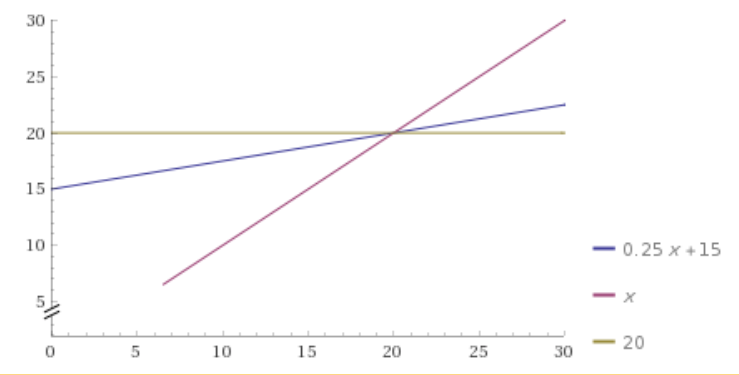
Den dritten Teil der ersten Frage, wo überall dasselbe bezahlen, kann man mit dem Schnittpunkt der drei Kostenfunktionen beantworten, also 20 * 100 MB.

2)

Die Grossmutter wird den Tarif nehmen, der bei 200 MB am billigsten ist. In meiner Graphik ist das die lilafarbene Linie (dritte Spalte in Deiner Tabelle).