Integral - Flächeninhalt halbieren mit einer Geraden, die parallel zur y-Achse verläuft

Question

Ich sitze hier grad an einem Problem, und zwar weiß ich nicht wie ich weiter vorgehen soll.

Also wie folgt: Es ist eine Funktion gegeben ( die Extrema befinden sich oberhalb der x-Achse ). Jetzt ist es so, dass dieser Graph der Funktion mit den Koordinatenachsen und der ( vertikalen bzw. Parallel zur Y-Achse ) Geraden mit der Gleichung ( z.B. x=65 ) ein Flächenstück einschließt. Hoffe man erkennt was ich meine, zusätzlich mit meiner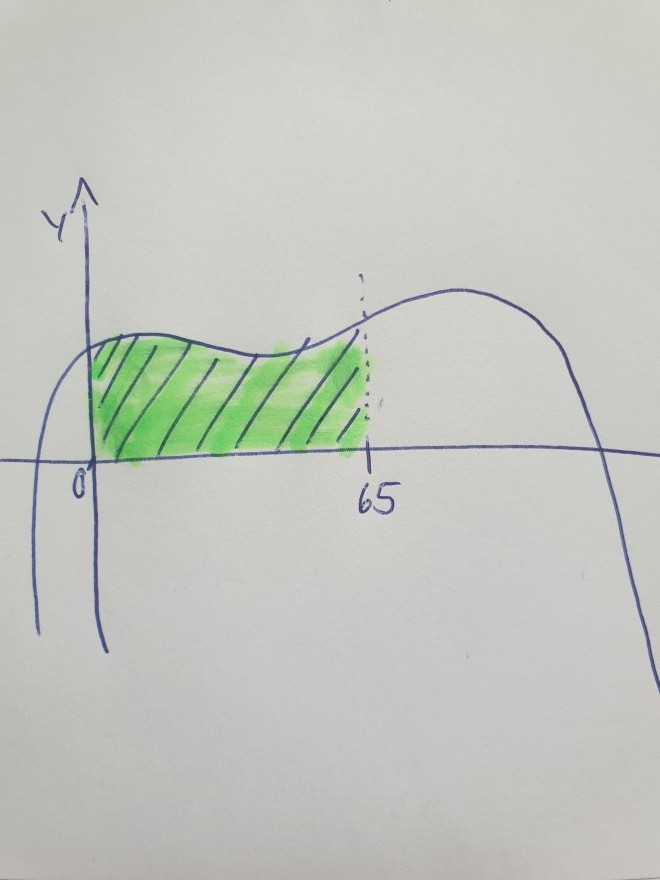

Text erkannt:

\( 8^{-8} \)

Zeichnung.

Man solle nun eine Gleichung der Geraden aufstellen, welche parallel zur y-Achse verläuft und diese Fläche durch 2 teilt.

Mein Ansatz: Erstmal Integral bilden, also mit unterer Grenze 0 und oberer Grenze 65. Dann mit dem Rechner ausrechnen lassen, damit man die Fläche hat. Dieses Flächenstück nun durch 2 teilen, damit man die Hälfte der Fläche hat. Und nun? Ich weiß jetzt nicht wie ich fortfahren soll.

Danke

Answer 1

Aloha :)

Leider hast du den Funktionsterm \(f(x)\) nicht mitgeteilt, daher hier nur die allgemeine Antwort:

1) Berechne eine Stammfunktion:$$F(x)=\int f(x)\,dx$$2) Berechne die Fläche \(A\):$$A=F(65)-F(0)$$3) Bestimme nun die Gleichung der gesuchten Geraden \(x=x_h\) durch Lösen der Gleichung:$$\frac{A}{2}\stackrel{!}{=}F(x_h)-F(0)$$

Comments

Hallo, danke erstmal. Kann leider nicht den Funktionsterm angeben, da dieser Schreibgeschützt ist, glaube ich.

Also habe noch eine Frage zu Schritt 3) und zwar muss man dann sozusagen das F(0) dann rüber holen indem man dieses subtrahiert, damit dann F(x_h) alleine auf einer Seite steht? Also habe das gemacht und dann kommt ja raus: F(x_h) = A/2 (das F(0) fällt ja weg). Dann zuletzt den x_h mit dem GTR ausrechnen lassen?

---

Das \(F(0)\) muss auf die andere Seite, dazu musst du es auf beiden Seiten addieren:$$F(x_h)=\frac{A}{2}+F(0)$$Rechts hast du dann einen Zahlenwert und erhältst insgesamt eine Gleichung, die nur noch von \(x_h\) abhängt. Diese Gleichumg musst du nur noch lösen, z.B. mit einem GTR.

Du bist also auf dem richigen Weg.

---

(das F(0) fällt ja weg).

Woher willst du das wissen????

Da steht nicht 0, sondern F(0)!

Wenn ich dann vorhin noch lese

Dann mit dem Rechner ausrechnen lassen,

und jetzt

Dann zuletzt den xh mit dem GTR ausrechnen lassen?

habe ich so meine Zweifel, ob du jenseits des Taschenrechnereinsatzes ausreichend Durchblick hast.

Wie lautet die zu integrierende Funktion? Es gibt keine "schreibgeschützen Funktionsterme". SCHREIBE SELBST!

---

Es ist ja zumindest schön, dass ihr beide (rk und Tsch) auf derselben falschen Wellenlänge schwimmt.

---

Vergiss meinen obigen Kommentar

---

danke, hoffe ihr hattet Spaß