Hallo Marco,
Mein Ansatz
z Achse bedeutet: Stützvektor (8/1/0) soll nur die z Achse beinhalten also --> (0/0/0)
Eine Parameterform der Ebene zu bestimmen ist einfach. Den Richtungsvektor der Geraden kannst Du sofort wiederverwenden. Da die Z-Achse enthalten sein soll, ist ein weiterer Richtungsvektor \(\begin{pmatrix} 0 & 0 & 1\end{pmatrix}^T\). Und wenn die Z-Achse enthalten ist, so ist auch der 0-Punkt enhalten. Wir können also den Stützpunkt mit \(\begin{pmatrix} 0 & 0 & 0\end{pmatrix}^T\) gleich weglassen. Die Ebene ist dann:
$$E: \space \vec{x} = r \cdot \begin{pmatrix} 1\\-8\\ 3 \end{pmatrix} + s \cdot \begin{pmatrix} 0\\0\\ 1 \end{pmatrix}$$
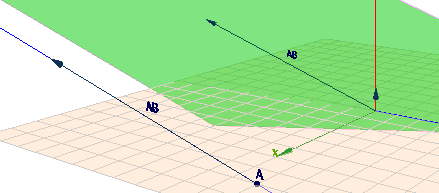
(klick auf das Bild und bewege die Szene mit der Maus)
Und hier die Lösung für die Normalenform der Ebene:
Wenn die gesuchte Ebene \(E\) die Z-Achse soll, dann muss die Z-Koordinate ihres Normalenvektor =0 sein! Weiter muss die Projektion des Richtungsvektors auf die XY-Ebene senkrecht auf dem Normalenvektor stehen. Folgende Szene soll dies veranschaulichen.
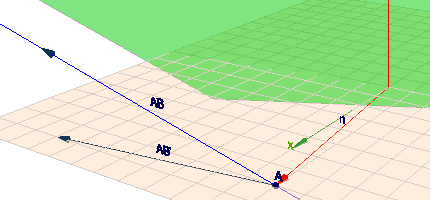
(klick auf das Bild und bewege die Szene mit der Maus) Dort siehst Du die Gerade mit ihrem Richtungsvektor \(\vec{AB}\) und dessen Projektion \(\vec{AB}'\) auf die XY-Ebene. Dass \(\vec{n}\) auf die Gerade zeigt ist hier Zufall, dass muss nicht so sein!
Diese Projektion erhält man, indem man die Z-Koordinate zu 0 setzt \(\rightarrow \begin{pmatrix} 1&-8& 0 \end{pmatrix}^T\) und einen Vektor, der senkrecht darauf steht, erhält man, indem man die verbleibenden Koordinaten vertauscht und einen negiert. $$\vec{n} = \begin{pmatrix} 8\\1\\ 0 \end{pmatrix}$$ Und mit der Z-Achse enthält sie auch den Ursprung; d.h. \(d=0\). Demnach hat die gesuchte Ebene \(E\) die Form $$E: \space \begin{pmatrix} 8\\ 1 \\ 0 \end{pmatrix} \cdot \vec{x} = 0$$ Gruß Werner