Grafisches Ableiten - von f'(x) zu f(x)

Question

Aufgabe:

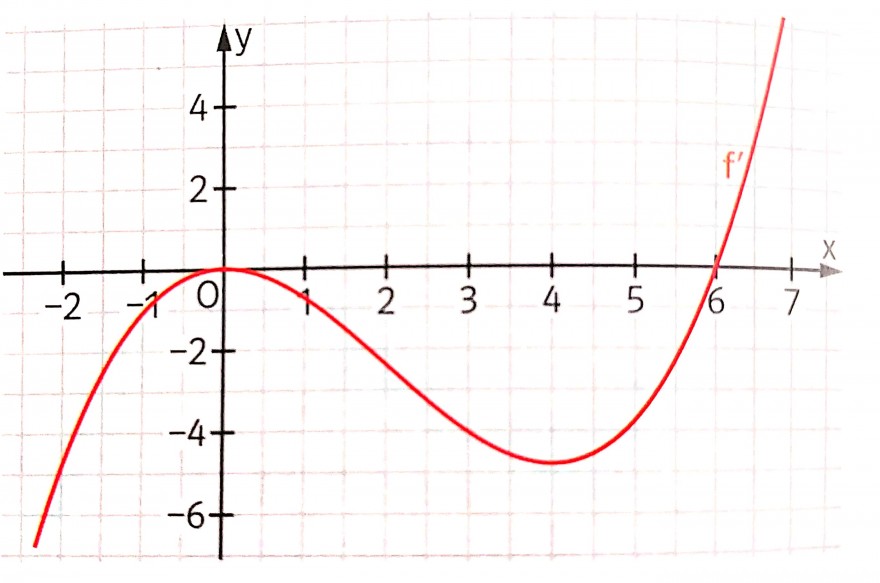
Zeichnen Sie die Ausgangsfunktion der Ableitung. Welche der folgenden Aussagen ist richtig?

1) f hat auf den Intervall [-2;7] zwei Extremstellen.

2) f ist auf dem Intervall [0;6] monoton fallend.

3) Auf dem Intervall [-2;7] hat der Graph von f einen Sattelpunkt.

4) f'' ist an der Stelle x=5 positiv.

5) f''' ist an der Stelle x=0 positiv.

Problem/Ansatz:

Da wo f'(x) einen Hoch- oder Tiefpunkt hat, hat f(x) einen Wendepunkt. In dem Fall wäre das bei (0/0) und (4/-5). Aber da wo f'(x) die x-Achse schneidet bzw. Nullstellen hat, hat f(x) Extremstellen. Also bei dieser Aufgabe bei (0/0) und (6/0).

Wie sieht die Ausgangsfunktion also aus, wenn sie bei (0/0) einen Wendepunkt und gleichzeitig eine Extremstelle haben muss?

Answer 1

Eigentlich hast du das doch schon gut beschrieben.

Einen Sattelpunkt bei 0 wegen einer zweifachen Nullstelle und einen Tiefpunkt bei 6 wegen der einfachen Nullstelle. Näherungsweise sieht das wie folgt aus

~plot~ 0.15*x^2*(x-6);0.0375x^4-0.3x^3;[[-5|10|-20|20]] ~plot~

Comments

Dankeschön, die Grafik hat mir sehr gut weitergeholfen! Ich hätte da aber trotzdem noch eine Frage. Eine der Aussagen ist "f'' ist an der Stelle x=5 positiv". Bei x=5 liegt bei f' und f ja ein Wendepunkt vor. Gibt es an dieser Stelle dann bei f'' einen Hochpunkt?

---

f''(5) > 0 bedeutet die Steigung von f' an der Stelle 5 ist positiv. a die Angegebene Funktion an der Stelle 5 steigt, ist diese Aussage wahr.

f''(5) > 0 bedeutet ebenso die Krümmung von f an der Stelle 5 ist linksgekrümmt. Auch das kann man an der Funktion schön ablesen.

Bei x=5 liegt bei f' und f ja ein Wendepunkt vor.

Diese Aussage ist Murks. f' hat an der Stelle 4 einen Tiefpunkt und damit hat f an der Stelle 4 einen Wendepunkt.

Answer 2

Der Graph der Ableitung hat die Gleichung f '(x)=a·x²·(x-6). Dann hat die Ausgangsfunktion f die Gleichung f(x)=\( \frac{a}{4} \) x⁴-2ax³+C und für a=1 sowie C=0 diesenVerlauf:

 Damit sollte es gehen.