Gegeben ist die Funktionenschar \( \mathrm{f}_{\mathrm{a}} \) mit \( f_{a}(x)=2 a^{2} \cdot x \cdot e^{-0,5 a x}(a>0) . \) Der Graph von \( f_{1} \)
und der Graph von \( \mathrm{f}_{1}^{\prime} \) sind in Fig. 1 dargestellt.
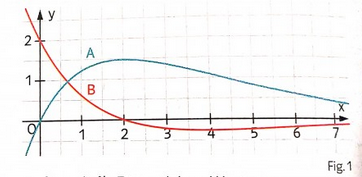
a) Begründen Sie, warum der Graph A aus Fig. 1 zur Funktion \( f_{1} \) und der Graph B zur Ableitungsfunktion \( \mathrm{f}_{1}^{\prime} \) gehört.
b) Berechnen Sie den Hochpunkt des Graphen von f in Abhängigkeit von a.
c) Berechnen Sie die Schnittpunkte der Graphen fa und f'a. Für welchen Wert von a schneiden sich die Graphen bei x = 0,5?
d) Die Punkte P (t | f2(t)) und Q (t | f'2(t)) verbinden für t > 0,5 eine Strecke, die parallel zur x-Achse verläuft. Berechnen Sie, für welchen Wert von t die Strecke am größten ist.
Problem/Ansatz:
fa(x) = 2a^2 * x * e^-0,5ax
f'a(x) = 2a^2 * e^-0,5ax + 2a^2x * e^-0,5ax (-0,5a) = e^-0,5a (2a^2 + (-1a^3x)
Zu b) Ich brauche eigentlich nur Hilfe bei der zweiten Ableitung. Hatte gedacht dass es f''a(x) = 2a^2 * e^-0,5ax + 2a^2 * e^-0,5ax (-0,5a) = e^-0,5ax (2a^2 + (- a^3) wäre, aber ich muss nachweisen dass es einen Hochpunkt gibt und das klappt irgendwie nicht. Ich habe auch bereits berechnen dass der HP bei x= 2/a und y= 4ae^-1 liegt, muss jetzt eben nur noch beweisen das es überhaupt einen HP gibt.
c) Hier habe ich beide Graphen gleichgesetzt, also:
2a^2*x*e^-0,5a = e^-0,5a (2a^2+(-1a^3)
Ich weiß aber jetzt nicht wie ich das nach x umstellen soll.
d) Die Aufgabe versteh ich gar nicht. Was muss man da machen?