Höhe eines Turms unter einem Böschungswinkel?

Question

Aufgabe:

Ein Aussichtsturm steht auf einem unter dem Böschungswinkel ε=6,5° ansteigenden ebenen Gelände. Um seine Höhe zu bestimmten, steckt man vor dem Turm eine Standlinie AB=100m ab, sodass A,B under Fußpunkt F des Turmes in einer Linie liegen. Von den Endpunkten der Standlinie misst man zur Turmspitze die Höhenwinkel α=21,4°und β =35,7°. Wie hoch ist der Turm.

2
\( \int \)

Problem/Ansatz:

Ich habe einfach keine Ahnung welchen "Satz" ich hier anwenden kann und welche Bedeutung hat dieser Böschungswinkel?

Answer 1

Ich habe einfach keine Ahnung welchen "Satz" ich hier anwenden kann und welche Bedeutung hat dieser Böschungswinkel?

Wenn du keine Ahnung hast solltest du dir zunächst eine Skizze anfertigen.

Zunächst zeichnest du also ein Gelände welches gegenüber der Horizontalen um 6,5° ansteigt. Warum dieser Winkel Böschungswinkel heißt, obwohl wir keine Böschung haben ist mir nicht ganz klar. Aber ich denke du solltest wissen was gemeint ist.

Wenn meine Skizze und Rechnung korrekt ist sollte der Turm ca. 51.11 m hoch sein.

x/SIN(14.9°) = 100/SIN(14.3°) → x = 104.1 m
h/SIN(29.2°) = 104.1/SIN(96.5°) → h = 51.11 m

Comments

Zunächst mal vielen Dank für deine Antwort. Prinzipiell habe ich eine Skizze gemacht, ich bin nur leider zu doof sie in meine Frage hochzuladen :o(

Leider habe ich auch keine Ahnung was es mit dieser Böschung auf sich hat, denn eine Steigung in einem ebenen Gelände ist doch gar nicht möglich, oder?

lG

---

"Eben" bedeutet du hast eine Ebene. Und diese kann gegenüber der Horizontalen ansteigen. Das Ebene Gelände muss also nicht waagerecht liegen.

Answer 2

Das sieht wohl so aus.

Damit müsste es doch klappen.

Sinussatz in den beiden Dreiecken. Der Innenwinkel

bei F ist bekannt 96,5° und der stumpfe Winkel bei B auch.

Kannst aber auch den Turm senkrecht nach unten bis auf

das 0-Niveau verlängern durch ein Stück x und auch von B aus

senkrecht runter bis zur 0_Linie

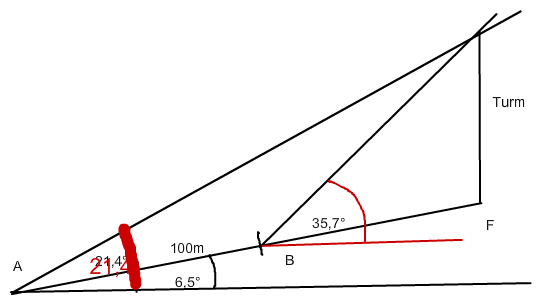
Text erkannt:

2

Comments

Perfekt!

Vielen Dank - ich tüftle weiter :o)

---

Etwas unklar ist mir noch, ob Höhenwinkel nicht grundsätzlich zur waagerechten gemessen werden anstatt zum Boden.

Ich habe sie jedenfalls zur waagerechten gemessen.

Vielleicht hast du deswegen die Winkelbögen weggelassen.

---

Ja, das ist wohl wirklich so, dass man die gegen die Waagerechte misst.

Ich versuche mal noch was zu ergänzen.

---

Vielen, lieben Dank!!!