Vergleich zu linearer Modellierung

Question

Aufgabe:

Die nebenstehende Tabelle zeigt die Wertentwicklung eines bestimmten Grundstücks in den letzten 10 Jahren.

a. Ist in diesem Falle eine lineare oder eine exponentielle Modellierung sinnvoller?

Geben Sie für die geeignete Modellierung alle relevanten Parameter an!

Geben Sie die geeignete Wachstumsfunktion (mit Legende) an!

b. Wie viel würde das Grundstück im Jahr 2030 kosten?

c. Wann müsste man ca. 100.000 Euro für das Grundstück bezahlen?

Problem/Ansatz:

Bitte um Erklärung des Rechnungsweges und der Lösungen von a. b. und c. !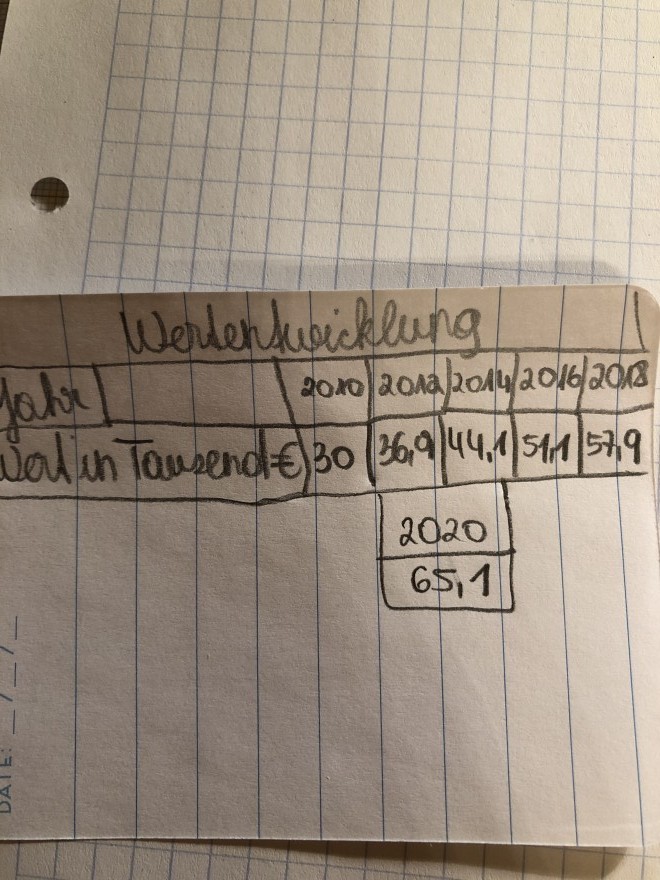

Text erkannt:

\( \frac{\frac{8}{3} \frac{x}{\frac{x}{3}}}{\frac{5}{3}} \)

Answer 1

Also für mich sieht das ziemlich linear aus:

Bleibt noch die Frage, ob Ihr schon eine Regressionsgleichung aufstellen könnt oder Du einfach eine Gerade durch den ersten und letzten Datenpunkt ziehen willst.

Comments

Ich muss nur das lösen was bei a) b) und c) steht! Könntest du mir da eventuell bitte helfen?  Wäre dringend:)

---

Wenn Du die von mir gestellte Frage beantworten würdest, wäre klar in welche Richtung die Lösung gehen soll.

---

Die Regressionsgleichung kann ich noch nicht lösen.

---

Die Frage war nicht nach lösen, sondern nach aufstellen. Also nicht. Fühlst Du Dich in der Lage, eine Gerade durch den ersten und letzten Datenpunkt zu ziehen?

---

Ja, denk schon

---

Na dann stell einfach diese lineare Gleichung auf.

---

Allgemeine lineare Gleichung: \(f(x)=m\cdot x+n\), wobei m den Anstieg und n den y-Achsenabschnitt darstellt.

Was mit Legende der Funktion gemeint ist weiß ich nicht.

---

ich schon... wir sind dran.

---

Alles klar, viel Erfolg euch! :-)

Answer 2

Anbei habe ich mal durch den ersten und letzten Punkt eine lineare und exponentielle Funktion modelliert.

~plot~ {0|30};{2|36.9};{4|44.1};{6|51.1};{8|57.9};{10|65.1};(65.1-30)/10*x+30;30*((65.1/30)^(1/10))^x;[[-1|22|0|120]] ~plot~

Du solltest jetzt sehen welche Modellierung besser passt.

Auch Aufgabe b) und c) solltest du jetzt schon grafisch näherungsweise bestimmen können.

Comments

Also ist die Formel f(x)=10•x+30.

Für b) muss ich dann 2030=10•x+30 rechnen,dass wären dann 200 Tausend Euro. Stimmt das?   und bei c) stehe ich an.

---

Also ist die Formel f(x)=10•x+30.

Das kann nicht sein. Dann würde gelten:

f(10) = 10*10 + 30 = 130

Das sieht man das das nicht passt oder?

Und fang nicht mit b) oder c) an wenn a) noch nicht richtig ist.

---

d ist ja der Abschnitt auf der y-Achse also 30 oder?

Und d ist die Steigung also 7,0 oder 7,2 oder nicht? Weil 36,9+7,2=44,1 und 44,1+7,0=51,1,also weiß ich nicht ob es stimmt oder mein Ansatz falsch ist

---

d ist ja der Abschnitt auf der y-Achse also 30 oder?

Und d ist die Steigung also 7,0 oder 7,2 oder nicht?

Zunächst mal darfst du nicht für unterschiedliche Dinge gleiche Buchstaben nehmen.

Ich weiß nicht wie ihr die lineare Funktion notiert. Üblich ist

y = ax + b
y = mx + b
y = mx + n

b oder n ist dabei der y-Achsenabschnitt. Der ist auch mit 30 richtig.

a oder m ist dabei die Steigung. Die ist mit 7 oder 7.2 verkehrt.

---

Auf die Steigung komme ich nicht.

---

y = mx + b

Wenn du b und einen Punkt P(x | y) kennst, könntest du die drei Sachen einsetzen und nach der Steigung m auflösen.

m = (y - b) / x

---

Und welche Punkte muss ich für x und y einsetzen,weil b ist ja 30

---

Ich habe den am weitesten rechts befindlichen Punkt genommen. Also den für das Jahr 2020.

---

Also (65,1-30)/ x

Aber was ist x jetzt?? Oder wie stellt man das auf?

---

Stimmt f(x)=0,5*x+30   ???

---

f(10) soll 65.1 sein. Stimmt das?

---

Bei 2020 liegt der Wert bei 65,1 im Bezug auf die Wertentwicklung eines Grundstücks in den letzten 10 jahren