Halllo limonade,
Welche Formel verwendet man dafür ?
Die Frage nach der Formel ist wie immer der falsche Weg. Die Frage müßte lauten: was siehst Du da oben in der Skizze? Kannst Du das auf bekannte Strukturen zurück führen.
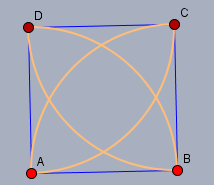
Berechne von der Figur im Quadratden Umfang (Orange Linien)
Die Länge der orangen Kreisabschnitte sind vier Viertelkreise. Demnach ist ihre Gesamtlänge identisch mit dem Umfang eines Kreises vom Radius der Quadratseite - und den Kreisumfang kennst Du!
Mit 'Umfang' würde ich das aber nicht bezeichnen!
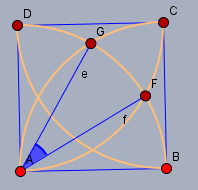
Wenn man den Umfang sucht, so müste man doch die Kreissegemente innerhalb der Figur weglassen (z.B. zwischen den Punkten \(F\) und \(G\)) - oder? Der Winkel \(\angle FAG\) sind genau \(30°\) - warum? \(30°\) sind der 12'te Teil eines Vollkreises. Vier davon sind \(4/12 = 1/3\) des Vollkreises. Verbleiben für den Umfang \(U\) der Figur$$U = \left(1 - \frac 13\right) U_{Kreis} = \frac 43 \pi r$$
Berechne anschliessend die schraffierte Fläche.
Suche auch hier nach bekannten. Die Kunst besteht u.U. darin, etwas weg zu lassen
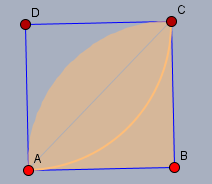
was siehst Du da oben? Das ist ein Viertelkreis - und seine Fläche ist ein Viertel eines Vollkreises. Nun denke Dir die gleiche Figur zwischen den Punkten \(D\), \(A\) und \(C\). Wenn Du das dazu zählst, dann ist die Fläche \(A^*\) in der Mitte doppelt belegt - also diese Linse zwichen den Punkten \(A\) und \(C\) . Folglich ist $$A^* = 2 \cdot \frac 14 A_{Kreis} - A_{Quadrat}$$Und die gesuchte Fläche \(A\), die Du oben sschraffiert hast, ist doch genau die Different vom Quadrat zu \(A^*\) - also:$$A = A_{Quadrat} - A^* = A_{Quadrat} - \left( \frac 12 A_{Kreis} - A_{Quadrat}\right) = 2 A_{Quadrat} - \frac 12 A_{Kreis}$$ Alles klar?
Nachtrag:
Die Kunst kann auch darin bestehen, etwas hinzuzufügen:
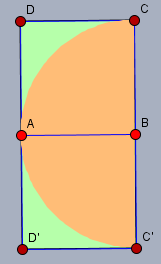
Wie groß ist die grüne Fläche?