Wo liegen alle Punkte die von 2 Punkten den gleichen Abstand haben?
Richtig. Auf einer Mittelsenkrechten zwischen den Punkten. D.h. bestimme die Mittelsenkrechte von A und B und schneide die mit dem Kreis.
MAB = 1/2 * (A + B) = [-1, 5]
AB = B - A = [2, 3] - [-4, 7] = [6, -4] = 2 * [3, -2]
Senkrecht zu AB ist [2, 3]
g: [-1, 5] + r * [2, 3] = [2·r - 1, 3·r + 5]
Das setze ich in die Kreisgleichung ein.
(x - 1)^2 + (y + 5)^2 = 65
((2·r - 1) - 1)^2 + ((3·r + 5) + 5)^2 = 65
r = -3 ∨ r = -1
Also sind die Punkte
[2·(-3) - 1, 3·(-3) + 5] = [-7, -4]
[2·(-1) - 1, 3·(-1) + 5] = [-3, 2]
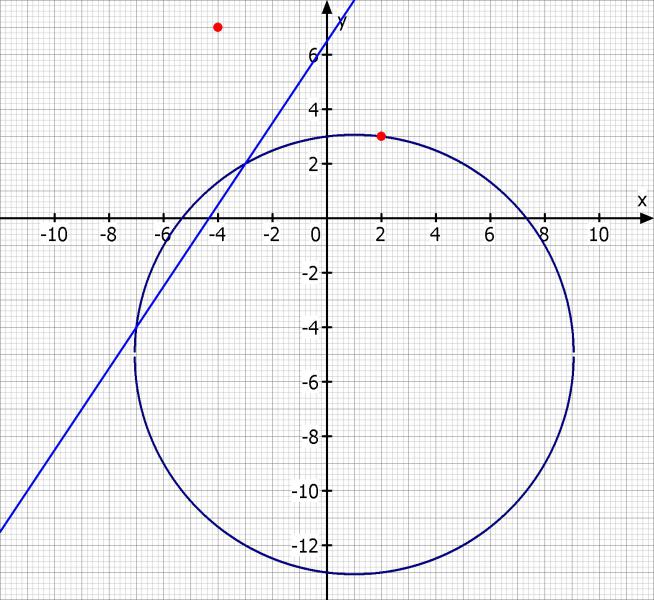
Skizze: