Problemlösendes Verhalten soll an folgender Aufgabe demonstriert werden:
Von einem inneren Punkt P eines gleichseitigen Dreiecks ABC sind die Abstände zu den Eckpunkten a, b und √(a^2+b^2 ). Welche Seitenlänge hat dann das gleichseitige Dreieck?
Es ist klar, dass die gegebenen Abstände von P zu den Eckpunkten die Seitenlägen eines rechtwinkligen Dreiecks bilden.
Da wir nicht wissen, wie man diese Aufgabe lösen kann, tun wir das Naheliegendste: Wir konstruieren ein Dreieck aus den drei gegebenen Abständen und spielen mit diesem ein wenig. Zum Beispiel drehen wir es so um einen Punkt außerhalb des Dreiecks, dass einer seiner Eckpunkte auf den benachbarten Eckpunkt fällt:
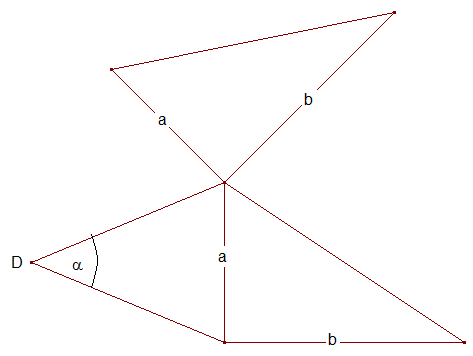
Auf diese Weise sind sechs Punkte A B C D A‘ und B‘ festgelegt. Unter diesen suchen wir einen, der von drei weiteren genau die gegebenen Abstände hat:
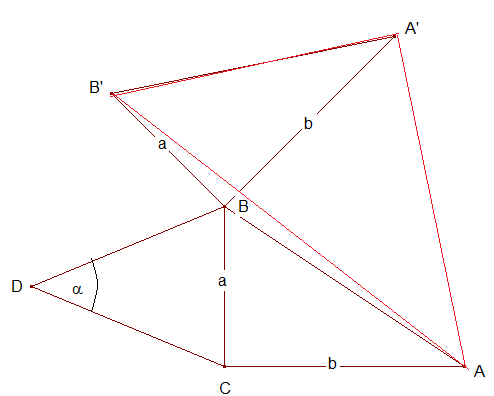
Dies leistet der Punkt B, der von A, A‘ bzw. B‘ die gegebenen Abstände hat. Leider ist das Dreieck AA’B‘ nicht gleichseitig und der Punkt B liegt nicht im Inneren von AA’B‘. Machen wir einen weiteren Versuch:
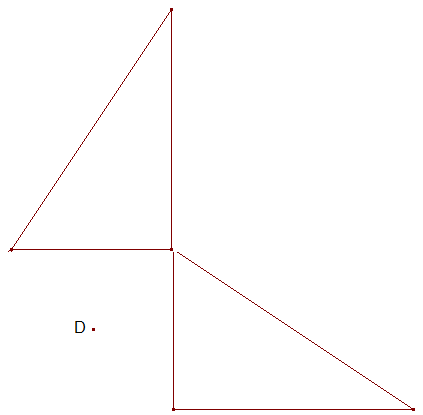
Auch hier hat B die drei gegebenen Abstände von drei weiteren Punkten und liegt sogar innerhalb des Dreiecks aus diesen drei Punkten. Aber das Dreieck ist wieder nicht gleichseitig.
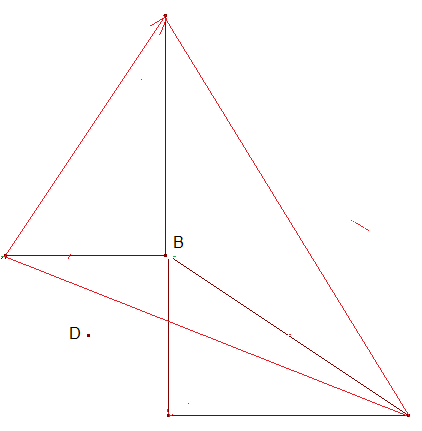
Wenn es überhaupt einen geeigneten Drehwinkel gibt, liegt dieser in der Größe zwischen den bisher gewählten Drehwinkeln. Möglicherweise wäre es eine gute Idee, den Abstand DB als einen der gegebenen Abstände zu wählen. Dann ist der Drehwinkel 60°:
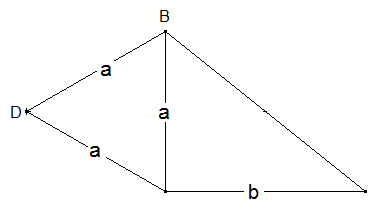
Und tatsächlich sind wir am Ziel:
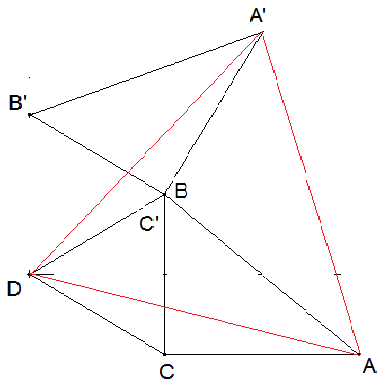
Dass nicht nur DCC‘ gleichseitig ist, sondern auch das Dreieck DAA‘ gleichseitig sein muss, lässt sich leicht begründen.
Nun zur Frage nach der Seitenlänge des zuletzt gefundenen Dreiecks DAA‘. Dazu legen wir das Dreieck ABC so in ein Koordinatensystem:
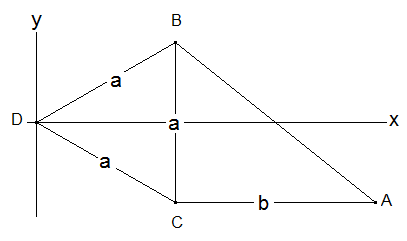
Wir wissen, dass DA die gesuchte Seitenlänge ist. Zu ihrer Berechnung brauchen wir die Koordinaten des Punktes A(a/2∙√3+b|-a/2). Dann berechnet sich die gesuchte Seitenlänge nach Pythagoras als
√((a/2∙√3+b)^2+(-a/2)^2 )=√(a^2+ab√3+b^2 )