In den vergangenen Tagen hat auf den Seiten der mathelounge ein Fragesteller immer wieder Aufgaben des Lehrbuches "Elemente der Mathematik für Sachsen", aus dem Westermann-Verlag eingestellt. Zusammenfassend kann man zu dem Ergebnis kommen, dass das Lehrbuch nicht geeignet ist, Schüler*innen einen Zugang zu einigen mathematischen Fragestellungen und Problemlösungen zu verschaffen. Im Folgenden versuche ich eine Kritik einiger der fraglichen Aufgaben.
Aufgabe 1:
Untersuche, ob der Umkreis der kleinste Kreis ist, der das Dreieck enthält. Beachte auch die verschiedenen Dreiecksarten. Beschreibe dein Ergebnis.
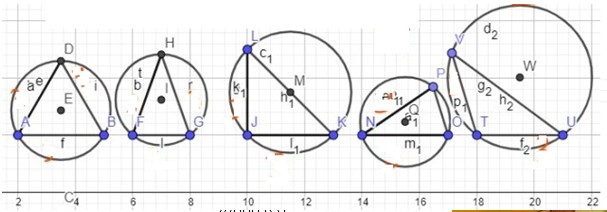
Kritik:
Hier soll eine Tatsache untersucht werden, die vielen Schüler*innen selbstverständlich erscheint und für die deshalb jegliches Problemverständnis fehlt. Die angefügte Skizze erhellt die Scheinproblematik nicht. Sie sollte wohl besser so ergänzt werden:
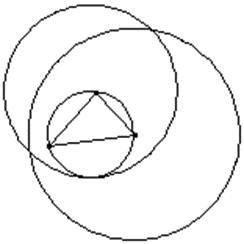
Aufgabe 2:
a) Betrachte das Bild (1) und vergleiche die Größe der abgebildeten Personen.
b) Im Bild (2) sind die gleichen Personen ohne perspektivischen Hintergrund zu sehen. Was stellst du fest?
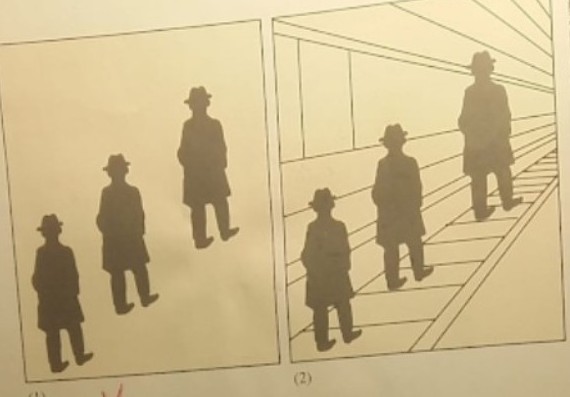
Bild (1) Bild (2)
Kritik:
Nebenbei sei erwähnt, dass in Fehler im Aufgabentext hier zusätzliche Verwirrung stiftet. Außerdem kann man dazu neigen, auch Bild (1) zentralperspektivisch zu sehen. Das Bild (2) hätte zusammen mit der Anweisung, die Größen mit einem Lineal zu messen, ausgereicht.
Aufgabe 3:
Rechts siehst du die Skizze eines Handballfeldes. Gewisse Regelverstöße werden mit einem 7-m-Wurf geahndet.
Zeichne für das Tor eine Strecke und konstruiere die 7-Meter-Marke. Beschreibe und begründe dein Vorgehen.

Kritik:
Die Aufgabe wäre in diesem Wortlaut klarer geworden:
Stelle das Tor im Maßstab 1:100 in deinem Heft dar und konstruiere dazu die 7-Meter-Marke. Beschreibe und begründe dein Vorgehen.
Aufgabe 4:

Ist es möglich die gesamte Bowle in einem 2-Liter-Krug zu servieren?
Begründe durch Rechnung.
Kritik:
Dieser Art Aufgaben hat unter dem Namen „Fermi-Aufgaben“ eine gewisse Bekanntheit erlangt. Hier sollen durch eigene Recherchen und Überlegungen fehlende Maßzahlen ergänzt werden. Wie soll das aber geschehen, wenn Dosen und Flaschen selbst in handelsüblichen Volumina in einer kaum überschaubaren Vielfalt existieren?
Aufgabe 5:
a) Was für eine Figur befindet sich im Strahlenbüschel unten? Miss nach.
b) Zeichne ein Strahlenbüschel und trage ein Trapez so ein, dass es als Quadrat erscheint.
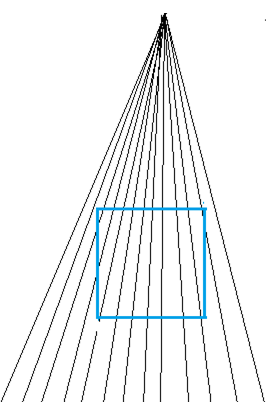
Kritik:
Zur Lösung von a) ist das Strahlenbüschel offenbar noch als bedeutungslos anzusehen. Unter b) taucht plötzlich der Begriff „erscheint“ auf, was wohl bedeuten soll, dass das Strahlenbüschel jetzt wie ein Büschel Hilfslinien der Zentralperspektive aufzufassen sei. Das sind aber nur Mutmaßungen, die ein Schüler nicht in jedem Falle ebenfalls anstellt. Dann ergibt die Aufgabe für ihn keinen Sinn.
Aufgabe 6:
Im Jahre 1991 hat die Bundesregierung eine Verpackungsverordnung erlassen. Was sagt sie aus?
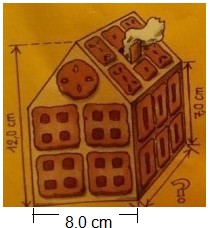
Pfefferkuchen werden oft in Schachteln verpackt, die die Form eines Hauses haben. Dieses Pfefferkuchenhaus soll mit 250 g Pfefferkuchen gefüllt werden.
Wie lang darf die Verpackung höchstens sein?
Kritik:
Die Dichte von Pfefferkuchen soll wohl ebenso geschätzt werden, wie der Volumenanteil unvermeidbarer Hohlräume. Das sind für meinen Geschmack zu viele Unwägbarkeiten.
Aufgabe 7:
Zum Schutz vor Straßenlärm wurde ein 340 m langer geradliniger Erdwall aufgeschüttet und mit Sträuchern bepflanzt. Bilde selbst geeignete Aufgaben und löse sie.
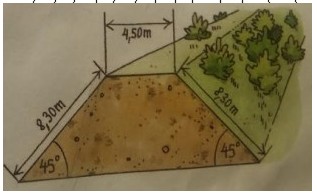
Fragenvorschlag des Lehrbuches: Wie viel Erde würde man sparen, wenn der Neigungswinkel auf 60 ° erhöht würde und die Höhe bei 5,87 m bleiben würde?
Kritik:
Auf den Fragenvorschlag des Lösungsteils zum Lehrbuch wird wohl kein*e Schüler*in von sich aus kommen. Wohl eher drängt sich folgende Frage auf: „Wie viele Büsche braucht man zur Bepflanzung des Lärmschutzwalles, wenn ein Busch pro m2 gepflanzt werden soll?
Aufgabe 8:
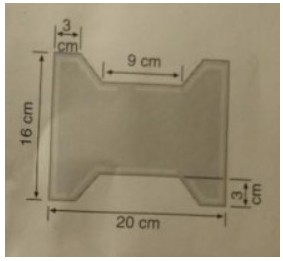
Einfahrten werden häufig mit Verbundsteinen gepflastert. Unten siehst du die Maße eines Steines, der 7 cm hoch ist. Er wird aus Beton hergestellt; 1 cm3 Beton wiegt 2,5 g
a) Eine 30 m2 große Einfahrt soll mit diesen Steinen gepflastert werden. Zur Sicherheit und wegen des Verschnittes werden 3% mehr Steine bestellt als mindestens nötig. Berechne, wie viele Steine bestellt werden müssen.
b) Ein gemieteter Kleinlaster hat eine Zuladung von 3t. Wie viele Fahrten sind für den Transport der benötigten Steine erforderlich?
Kritik:
Die gegebenen Abmessungen der Steine machen deren Verlegung mit Fugen unausweichlich. Falls die Fugen überall die gleiche Breite haben, beträgt die Fugenfläche mehr als 10% der Steinfläche. Dieser Umstand wäre bezüglich der Bestellung deutlich wichtiger als ein möglicher Verschnitt von 3%.
Fazit:
Selbst mancher Erwachsene, der über mehr Lebenserfahrung verfügt, als ein Jugendlicher, hätte mit derartigen Aufgabenstellungen seine Schwierigkeiten. Lebenserfahrungen sind aber für die Lösungen einiger dieser Aufgaben eine unerlässliche Voraussetzung. Insbesondere die Aufgaben zur Zentralperspektive sind wenig geeignet, erste Erfahrungen mit dieser Darstellungsart zu erwerben.