Den mathematischen Begriff ‚Bruch‘ führt der Didaktiker Steinbring folgendermaßen ein:
Aufgabe 1:
Nenne verschiedene Worte, die den Wortbestandteil ‚-bruch‘ haben.
Schülerlösungen:
Wolkenbruch, Einbruch, Ausbruch, Dammbruch, Anbruch, Waffelbruch, Beinbruch, …, Bruchstück.
Aufgabe 2:
Bilde Sätze mit dem Wort ‚Bruchstück‘.
Schülerlösung:
Ein Blumentopf ist heruntergefallen und in Bruchstücke zersprungen.
Aufgabe 3:
Ist das grau unterlegte Bruchstück ein Viertel des Kreises?
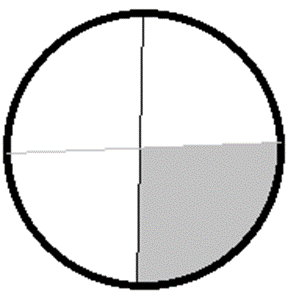
Schülerlösung:
a) Ja, so ungefähr. b) Nein, die anderen drei Viertel müssen ebenso groß sein, wie das grau unterlegte Stück.
Bemerkungen zu dieser Einführung des mathematischen Begriffes ‚Bruch‘:
Steinbring will offensichtlich das umgangssprachliche Verständnis des Bruchbegriffes vom mathematischen Bruchbegriff abgrenzen. Aber ist das wirklich erforderlich? Die weitaus meisten mathematischen Begriffe sind umgangssprachlich unbesetzt. Diese werden in der Schule mit einem Definitionstext eingeführt, dessen inhaltliche Bedeutung anhand von Beispielen und Gegenbeispielen vertieft wird. Warum sollte man mit umgangssprachlich besetzten Begriffen nicht genauso verfahren? Immerhin zeigt Steinbring in Aufgabe 3 ein Gegenbeispiel zum mathematischen Begriff ‚ein Viertel‘. Dies geschieht allerdings ohne vorherige Klärung des Begriffes ‚ein Viertel‘ in der Mathematik durch den Lehrer. Zum Glück weiß ein Schüler, dass ein Ganzes in vier gleichgroße Teile zerlegt werden muss, damit in der Mathematik jedes davon ‚ein Viertel‘ genannt werden darf. Der Übergang von der Umgangssprache in die Sprache der Mathematik ist dem Schüler offenbar zugeflogen - vielleicht weil er weiß, dass er sich in einer Mathematikstunde befindet. Ob allen SuS einer Klasse dieser Übergang nun auch gelungen ist, klärt Steinbring nicht.
Das Prinzip des Teilens kennen die SuS lange bevor Brüche eingeführt werden. Sie verstehen darunter intuitiv ein gerechtes Teilen. Ein entsprechendes Verständnis veranlasst SuS dazu, eine Pizza gerecht unter 4 Personen aufzuteilen:
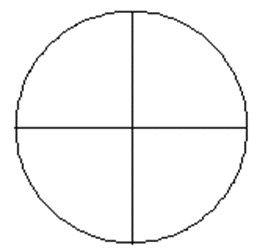
Der Unterschied zwischen Umgangssprache und mathematischer Sprache bezüglich des Begriffes ‚Teil‘ wird SuS schlagartig deutlich, wenn der Aspekt des gerechten Teilens benannt wird. Der Umweg über die Aufgaben 1 und 2 ist nicht erforderlich. Eher kann diese Einführung bei einigen SuS zur Verwirrung führen. Im Kern geht es um der Unterschied zwischen ‚Bruch‘ als Ergebnis eines von Zufällen begleiteten Zerbrechens und den Begriff ‚Bruch‘ als gerechter Anteil an einem Ganzen - also um eine Aufteilung des Ganzen in gleichgroße Teile. Dieser Unterschied muss nicht von SuS selbständig herausgearbeitet werden, um verstanden zu werden. Der Unterschied ist jedem Kind unmittelbar klar.
Quelle:
Die Konstruktion epistemologischer Dreiecke zur Analyse von Begriffsdeutungen bei mathematischen Lückentexten (hal.science)
