Aufgabe:
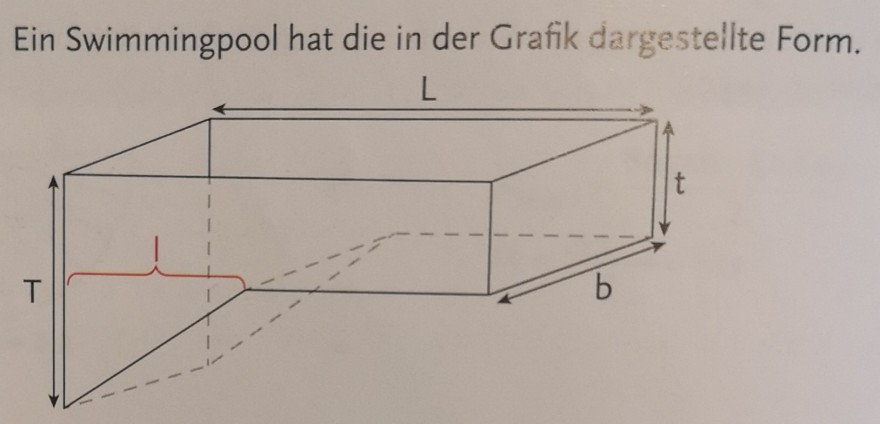
Ein Swimmingpool hat die in der Grafik dargesteilte Form.
Sandro und Marina erstellen eine Formel zur Berechnung des Fassungsvermögens des Pools. Sie lösen das Problem auf unterschiedliche Weise und erhalten folgende Formeln.
Sandro: \( V=\frac{(t+T) \cdot I}{2} \cdot b+b \cdot t \cdot(L-I) \)
Marina: \( \quad V=\frac{(T-t) \cdot I \cdot b}{2}+L \cdot b \cdot t \)
a) Interpretieren Sie die aufgestellten Formeln jeweils in Bezug auf die zugrunde liegende Unterteilung des Pools in Teilkörper.
b) Zeigen Sie durch entsprechende Umformungen, dass die beiden Formeln äquivalent sind.
Die Abmessungen des Pools betragen:
\( \mathrm{b}=12,5 \mathrm{m}, I=17 \mathrm{m}, \mathrm{L}=25 \mathrm{m}, \mathrm{t}=0,9 \mathrm{m}, \mathrm{T}=3 \mathrm{m} \)
c) Die Seitenwände des Pools werden neu gestrichen. Berechnen Sie, für wie viel Quadratmeter Farbe gekauft werden muss.
d) Der Pool wird mit Wasser gefüllt. Berechnen Sie, wie lange die Füllung dauert, wenn die Wasseroberfläche \( 10 \mathrm{cm} \) unterhalb des Beckenrands liegen soll und pro Stunde 10 Kubikmeter Wasser in den Pool fließen.
Lösungen:
Sandro unterteilt das Becken in ein Prisma mit trapezformiger Grundfläche mit der Höhe b und einen Quader (Beckenbereich mit der Tiefe \( t \) ). Marina unterteilt das Becken horizontal in ein Prisma mit dreieckiger Grundfläche und der Höhe b und einem darauf liegenden Quader mit der Länge L, Breite b und der Höhe t.
Sandro: \( V=\frac{(t+T) \cdot I}{2} \cdot b+b \cdot t \cdot(L-I) \)
\(= b \cdot\left(\frac{t \cdot I}{2}+\frac{T \cdot I}{2}+t \cdot L-t \cdot I\right)=b \cdot\left(\frac{T \cdot I}{2}+t \cdot L-\frac{t \cdot I}{2}\right) \)
Marina: \( V=\frac{(T-t) \cdot I \cdot b}{2}+L \cdot b \cdot t=b \cdot\left(\frac{T \cdot I}{2}-\frac{t \cdot I}{2}+t \cdot L\right) \)
c) Es müssen fur \( 129,45 \mathrm{m}^{2} \) Farbe gekauft werden.
d) \( t=0,9-0,1=0,8 \mathrm{m} \) und \( T=3-0,1=2,9 \mathrm{m} \)
\( V=473,13 \mathrm{m}^{3} \)
Dauer \( 47.31 \mathrm{h}=1 \) Tag 23 Stunden und 19 Minuten
Problem/Ansatz:
Bitte um Hilfe, ich Verstehe a überhaupt nicht
