Wie berechne ich den Spurpunkt?

Question

Aufgabe:

In Richtung des Vektors (-1|-3|1) fällt paralleles Licht.

Im 1 Oktanden des Koordinatensystems steht die senkrechte Strecke PQ mit P( 4|6|0) und Q(4|6|3). Konstruieren Sie das Schattenbild der Strecke (zeichnerisch und rechnerisch).

Problem/Ansatz:

Ich habe die Geradengleichung bestimmt. Diese lautet g:x= (4|6|3)+r(-1|-3|1).

Dann habe ich für den Sxz y=0 gesetzt ⇔ 6-3r=0 ⇔r=2. Das habe ich dann in die Gleichung eingesetzt und für Sxz (2|0|5) raus, aber nun komme ich nicht weiter, denn normalerweise müsste man die z Koordinate durch eine 0 ersetzen und hier macht es keinen Sinn. Ich würde mich freuen, wenn mir jemand weiterhelfen könnte.

Comments

Schaue Dir die Szene an und entscheide selbst ;-) Deine Rechnung ist richtig.

---

Vielen Dank für Ihre Hilfe! :)

Answer 1

[4, 6, 3] + r * [1, 3, -1] = [x, y, 0] --> x = 7 ∧ y = 15 ∧ r = 3

[4, 6, 0] + r * [-1, -3, 1] = [x, 0, z] → x = 2 ∧ z = 2 ∧ r = 2
[4, 6, 3] + r * [-1, -3, 1] = [x, 0, z] --> x = 2 ∧ z = 5 ∧ r = 2

[4, 6, 0] + r * [-1, -3, 1] = [0, y, z] → y = -6 ∧ z = 4 ∧ r = 4
[4, 6, 3] + r * [-1, -3, 1] = [0, y, z] → y = -6 ∧ z = 7 ∧ r = 4

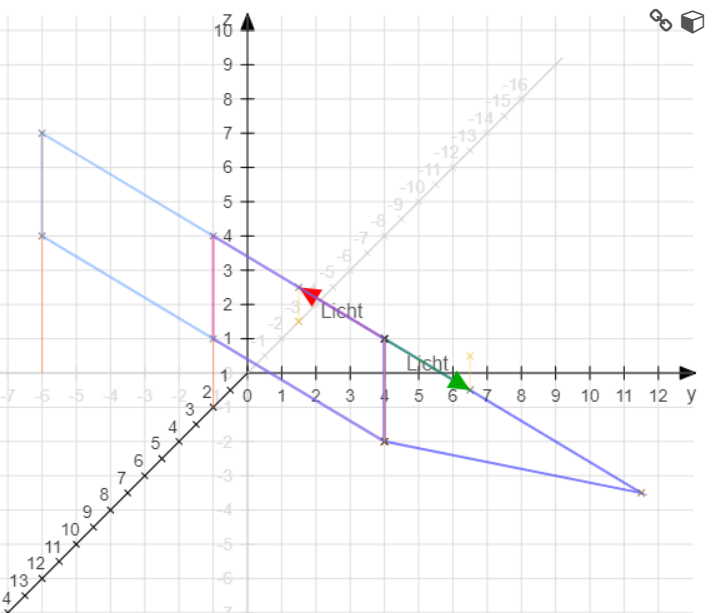
Hier die Skizze, je nachdem an welcher Ebene der Schatten entsteht.

Answer 2

Hallo

 welchen Schatten willst du denn? den auf dem Boden also z=9 oder auf der "Wand" y=0 du hast den Schattenpunkt der Spitze auf dieser Wand bestimmt, der Fußpunkt liegt dann da wo z=0 ist

Gruß lul

Comments

Da das in der Aufgabe nicht explizit genannt wurde, denke ich, dass man beide Schatten meint. Woher weiß man, dass z=9 ist. Muss z nicht gleich 0 sein?

---

sorry z=9 war ein Tipfehler, also es war z=0 gemeint.

lul