Aufgabe:
Mit einem Steigrohr soll Wasser aus einer 2 m tiefer gelegen Stelle abgesaugt werden. Um wieviel Prozent muss der innere Querschnitt eines Durchflussrohres mit 4 cm Innendurchmesser mittels einer Stauschraube mindestens vermindert werden, damit an der Engstelle bei einem Durchfluss von 5 l je Sekunde ein ausreichender Unterdruck zum Absaugen des Wassers entsteht?
Anmerkungen:
a) Hier muss eine Saughöhe von \( 2 \mathrm{~m} \) aberwunden und der dazu gehorige Unterdruck bestimmt werden. Also \( \Delta p=g \cdot h \cdot \rho \).
b) Die vorhandene Strömungsgeschwindigkeit \( v_{1} \) errechnet sich uber die Durchflussmenge pro Zeit und den gegebenen Rohrquerschnitt.
c) Uber die Gl. (21) erhalt man die notwendige Geschwindigkeit \( v_{2} \). Damit lasst sich dann der gesuchte Quersehnitt \( \boldsymbol{A}_{2} \) bestimmen
d) Hinweis: Man hat auch die Moglichkeit, uber Gl. (23) zur gleichen Losung zu kommen, wenn man diese Gleichung nach \( A_{2} \) umstellt. Dies ist allerdings nicht sanz einfach.
Skizze:
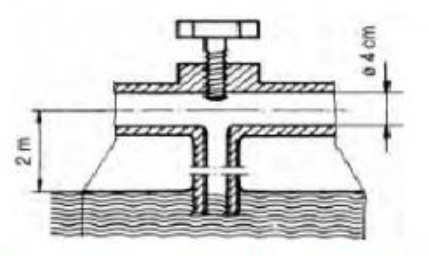
Zuerst habe ich den Unterdruck mit ausgerechnet Δp=g*h*ρ=9,81m/s2 *2m*1000=19620 bar
Dann den großen Rohrquerschnitt mit 0,001257qm.
Dann die Volumengeschwindigkeit v1 5000qqm/12,57qm mit 3,97m/s
Jetzt müsste ich mit der Bernoulli-Gleichung die Geschwindigkeit v2 ausrechnen um auf A2 zu kommen. da komm ich nicht mehr mit.