Hallo,
In der Aufgabe ist nach der Funktionsgleichung einer Parabel gesucht.
Die Skizze zu Deiner Aufgabe sieht in etwa so aus:
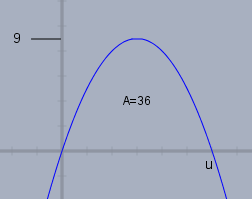
Was kann man da sehen? Die Parabel verläuft durch den Ursprung. D.h. der Punkt \((0;0)\) ist ein Punkt der Parabel. Der Hochpunkt (bzw. Scheitel) hat die Y-Koordinate \(y_s=9\). Die Fläche unter der Parabel zwischen den beiden Nullstellen ist 36.
Das ist alles gegeben und das reicht aus, um die Funktion eindeutig zu bestimmen.
1.Lösungsweg:
Der Weg über die allgemeine Form einer Parabel \(y(x) = ax^2 + bx + c \) ist etwas aufwendig. Daher nehme ich gleich die Scheitelpunktform. Die zweite Nullstelle liege bei \(u\) und es ist bekannt, dass der Scheitel einer Parabel immer in der Mitte zwischen den beiden Nullstellen liegt. Folglich ist die Position des Scheitels \(x_s=\frac u2\). Also lautet die Gleichung bis hierhin$$y(x) = a\left( x - \frac u2 \right)^2 + 9$$Da der Ursprung ein Punkt auf der Parabel ist, ist $$y(0) = 0 \\ \begin{aligned} \implies a\left( - \frac u2 \right)^2 + 9 &= 0 \\ au^2 &= -36\end{aligned}$$Um die Information über die Fläche zu nutzen, muss die Funktion integriert werden. Es ist$$\begin{aligned} \int_0^u a\left( x - \frac u2 \right)^2 + 9 \,\text dx &= 36 \\ \int_0^u ax^2 - aux + \frac 14 a {u^2} + 9 \,\text dx &= 36 \\ \left. \frac 13 ax^3 - \frac 12 aux^2 + \frac 14 au^2x + 9x\right|_0^u &= 36 \\ \frac 13 au^3 - \frac 12 au^3 + \frac 14 au^3 + 9u &= 36 \\ \frac 1{12} au^3 + 9u &= 36 &&\left| au^2 = -36 \space \text{s.o.}\right. \\ -3u + 9u &= 36 \\ 6u &= 36 \\ \implies u &= 6\end{aligned}$$und aus \(au^2 = -36\) folgt dann noch \(a=-1\). Einsetzen von \(u\) und \(a\) in die Formel für \(y(x)= \dots \) oben gibt dann die gesuchte Funktion $$y(x) = -(x-3)^2 + 9$$
2. Lösungsweg:
Wenn man weiß, dass die Fläche eines symmetrischen Parabelausschnitts gleich \(2/3\) der Fläche des umgebenden Rechtecks ist, so muss hier gelten$$\frac 23 \cdot 9 u = 36 \implies u = 6$$und aus der Bedingung \(y(0)=0\) folgte ja \(au^2 = -36\) (s.o.) - also ist \(a=-1\).
Gruß Werner