Parabel zeichnen im Koordinatensystem

Question

Am 4. Februar 2004 ging mit der Einweihung der 6,4 km langen Ortsumgehungsstraße für die Einwohner der Stadt Eilenburg ein lang gehegter Wunsch in Erfüllung. Diese Straße verläuft auf einem Damm mit insgesamt fünf Brücken.

Abbildung nicht maßstäblich.

Die längste Brücke führt über die Mulde und wurde als Bogenbrücke gebaut. Der Brückenbogen hat eine Spannweite von \( 54,30 \mathrm{m} \) und eine Scheitelhöhe von \( 15,00 \mathrm{m} \)
Im Koordinatensystem kann der Brückenbogen vereinfacht als nach unten geöffnete Parabel mit der Funktionsgleichung \( y=f(x)=a \cdot x^{2}+15(a \in R) \) dargestellt werden.

a) Skizzieren Sie diese nach unten geöffnete Parabel in einem Koordinatensystem. Kennzeichnen Sie den Scheitelpunkt mit S und die Schnittpunkte der Parabel mit der x-Achse mit \( P_{1} \) und \( P_{2} \). Geben Sie die Koordinaten der drei Punkte \( S \), \( P_{1} \) und \( P_{2} \) an.
b) Berechnen Sie den Wert von a in der Gleichung \( y=a \cdot x^{2}+15 \) und geben Sie diesen auf Hundertstel genau an.
c) Die Spannweite des Brückenbogens wird durch neun Verstrebungen in zehn gleichbreite Abschnitte unterteilt. Geben Sie die Länge der längsten Verstrebung an. Berechnen Sie die Länge der kürzesten Verstrebung.

Answer 1

Hallo

 die Frage ist schwer zu verstehen, du kannst a) eine wertetabelle machen, oder einfacher dir die Funktion mit einem Funktionsplotter zeichnen lassen, am besten löst du zuerst b) da du die Nullstellen bei +-halbe Spannweite kennst kannst du eine in f(x)=0 einsetzen und daraus a bestimmen, aber auch einfach eine Parabel von der du den Scheitel und die Nullstellen kennst zu zeichnen sollte dir gelingen,

c) einfach feststellen wo die längste und kürzeste Strebe steht und da f(x) berechnen.

Gruß lul

Answer 2

Hallo,

der Brückenbogen hat eine Spannweite von \(54,3\text m\) und eine Höhe von \(15\text m\). Das sieht in einer Zeichnung etwa so aus

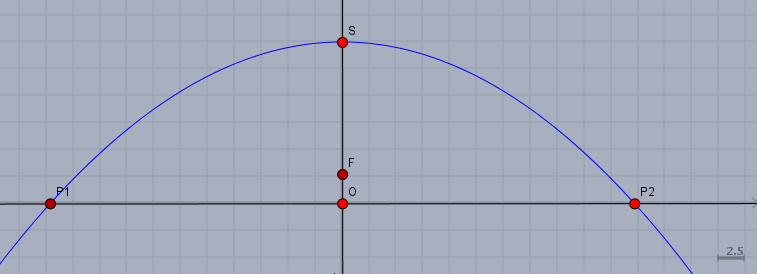
Mit einem Maßstab von 1:500 (d.h. 0,5 cm := 2,5m) kannst Du das bequem auf einer DINA4-Seite unterbringen. Die Position von \(S\) ist \(S=(0;\,15) \text m\) und die Positionen von \(P_1\) und \(P_2\) sind dann \(P_{1,2} = (\mp 27,15;\, 0  ) \text m\) bzw. \(( \mp5,43 \text{cm};\, 0)\) auf dem Papier.

Falls Du noch Fragen zu der Aufgabe hast, so melde Dich bitte. Zur Kontrolle: \(a \approx -0,02 \,\text m^{-1}\)