Meine Frage war, ob ein nach den Daten dieser Quelle
https://experience.arcgis.com/experience/09f821667ce64bf7be6f9f87457ed9aa
vorgeschlagenes Modell zur Corona-Epidemie in Schweden was taugt.
Alter Schwede!
Am 23.4. haben die Schweden die Statistik der beiden letzten Wochen - wohl durch Nachmeldungen aus den Provinzen - gegenüber den Daten vom 21.4 um bis zu 33% korrigiert. Die 3 letzten Tage hatte ich sowieso gleich weggelassen, weil ich mit Meldeverzögerungen rechnete. Weil die Änderungen aber so gravierend waren und man mit ähnlichen Korrekturen alle 2 Tage rechnen muss, war alles, was oben stand Makulatur! Deshalb habe ich es einfach gelöscht.

Deshalb muss alles nochmal neu überlegt werden:
Man kann erwarten, dass die Seuche ähnlich wie eine Kettenreaktion oder Hefevermehrung verläuft, zuerst ungefähr exponentiell, später begrenzt.
Bei der Kettenreaktion treffen zunächst immer 2 Neutronen auf spaltbare Atomkerme und jedes haut 2 neue Neutronen dort heraus, dann schlagen diese 2 Neutronen 4 heraus usw.. Dann aber fliegt die Bombe einen mm auseinander (social distancing) immer mehr Neutronen treffen schon auf gespaltenes Material oder auf nichts (Immune/Tote/keine weiteren Freunde vorhanden) und erzeugen keine 2 brauchbaren Neutronen mehr. Die Kettenreaktion verebbt. Sag statt Neutron Corona-Virus oder Infizierter:
Zähle in Schweden die Anzahl aller bis zum Zeitpunkt t Corona-Infizierten, I(t)
Dann sollte I(t) so aussehen:
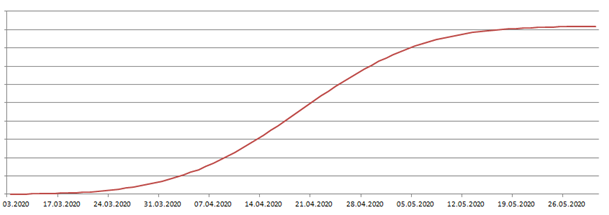
Bild 1
Wie kann man die Anzahl der Infizierten feststellen: geht zunächst nicht!
Man kann sie auch nicht abschätzen: Schweden hat 10 Mio Einwohner, 20 000 positiv getestete, dann gibt es also zwischen 20 000 und 10 Mio Infizierte.
Das einzige, was sicher ist, ist die Anzahl der Todesopfer. Wenn die Behandlung in Schweden überall etwa die gleiche Qualität hat, muss die Anzahl der Summe der Opfer zum Zeitpunkt t proportional zur Anzahl der Infizierten I(t-a) sein, mit a= mittlere Überlebensdauer eines Infizierten vom Tag der Infektion bis zum Todestag.
Also spiegelt die Anzahl der Toten/Tag = A(t) die Anzahl der Infizierten vor - sagen wir mal - 3 Wochen vor t wieder. Am 24.4. wurden folgende Werte für A(t) veröffentlicht:
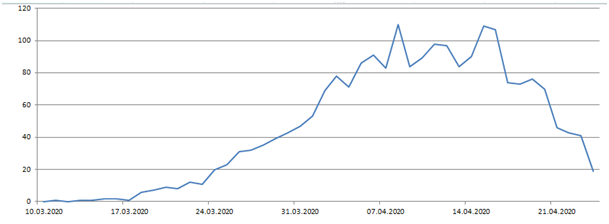
Bild 2
Leider ist das nicht die gesuchte Funktion, weil sie nur die bis zum 24.4. verfügbaren Daten enthält. Die Daten der beiden letzten Wochen sind zunächst unbrauchbar. Vergleichen wir die veröffentlichten Daten vom 21.4. und vom 24.4.
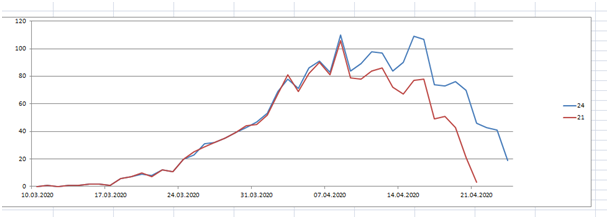
Bild 3
Man sieht, die jüngeren Daten wurden durch Nachmeldungen beträchtlich nach oben korrigiert, und zwar je jünger desto mehr.
Nehmen wir an, dass alle 3 Tage die Werte der jeweils letzten 2 Wochen so nach oben gehen, wie vom 21.4. bis 24.4.. Dann erhalten wir eine durch Schätzung korrigierte Liste, die die wahren Verhältnisse am 24.4. besser wiedergeben sollte, die grüne Kurve im nächsten Bild.

Bild 4
Da die (grüne) Kurve sehr unregelmäßig ist, bilden wir mal die Integralfunktion davon, um eine Glättung zu erzeugen.
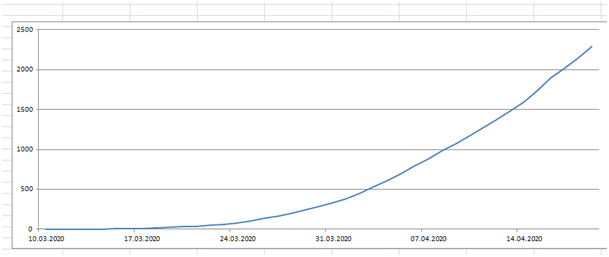
Bild 5
Da die Seuche in Schweden am Anfang der Epidemie exponentiell verlaufen sollte, versuchen wir mal eine Annäherung durch y = a exp(k*t)
Man sieht schon an den Verdopplungszeiten, dass das nicht geht (statt t=14, schreibe ich anschaulicher t=24.3.):
I(24.3.) = 81, I(27.3.) = 167, I(30.3.) = 284 < 334 zu wenig
I(3.4.) = 533, I(9.4.) = 1073, I(15.4.) = 1740 < 2146 zu wenig
Also nehmen wir eine bessere Funktion, die passt:
I(t) = k* Φ((t-µ)/σ) mit k=4600, µ=40,6, σ=13,5
Warum sollten die Sterbefälle über einer Zeitachse einer Normalverteilung folgen?
Weiß ich nicht, ist mir auch egal. Ich suche nur eine Funktion, mit der man leicht rechnen kann!
Verlängere ich jetzt einfach Aktiencharts? Mal sehen! 3 Beispiele:
Titius- Bode-Regel: war falsch; siehe Merkur, Neptun, sonstige Abweichungen
3. Kepler’sche Gesetz: war richtig. Der physikalische Beweis kam erst 70 Jahre später durch Newton
Hubble’sches Gesetz: war korrekt ohne Begründung. Er hat einfach eine lineare Regression gemacht.
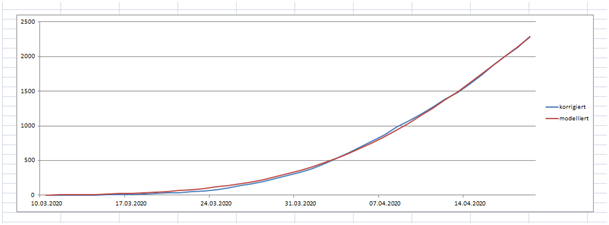
Bild 6
Da die modellierte Funktion so einfach ist und eigentlich nur 2 Parameter enthält und die Lage bis dato gut beschreibt, könnte man vermuten, dass sie auch die Zukunft gut beschreibt.
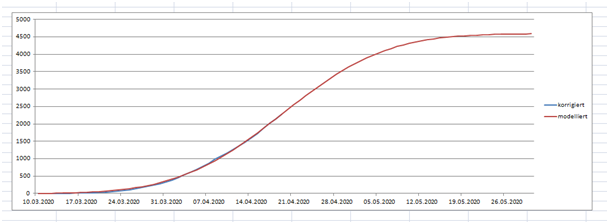
Bild 7
Folgerungen, an denen man das dann überprüfen kann:
Gesamtzahl der Corona-Toten bis 24.4. am 24.4. veröffentlicht: 2192
Prognose: Dieser Wert (bis 24.4.) wird in den nächsten 2 Wochen in der Statistik auf knapp 3000 hochkorrigiert, Zwischenergebnis: am 29./30.4 werden 2700 überschritten (für den Zeitraum bis 24.4.).
Machen wir mal die Ableitung zur Feststellung der Anzahl der tägl. Todesfälle:
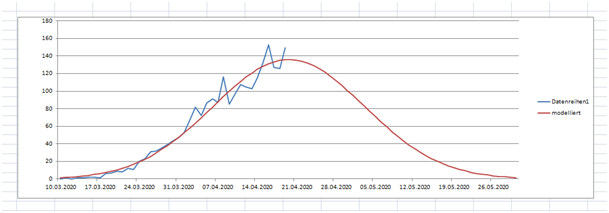
Bild 8
Prognose: Mitte Mai < 50, Ende Mai einstellig
Gesamtopferzahl: <5000
Herdenimmunität ist nicht genau definiert. Schweden als Ganzes scheint mir keine Herde zu sein. Die Zieldurchseuchung hängt bestimmt auch von der Häufigkeit und Intensität der Sozialkontakte ab. In der Mietskaserne oder im Asylantenwohnheim dürfte die Herdenimmunität bei einer größeren Prozentzahl erreicht werden als in Lönneberga.
Wenn man die Letalität von Heinsberg mit 0,0037 anwendet, hätten sich am Ende 1,2 Mio von 10 Mio Schweden infiziert, also 12% (sehr vage Schätzung, aber weit weg von 60%), in den Städten mehr als 12%, auf dem Land weniger.
Update 9.5.20:
Blau ist die summierte Anzahl der Sterbefälle jeweils bis dato auf Basis der korrigierten am 9.5. veröffentlichten Zahlen. Rot ist das Modell. Noch passt es zur Prognose: Mitte Mai < 50 Sterbefälle pro Tag
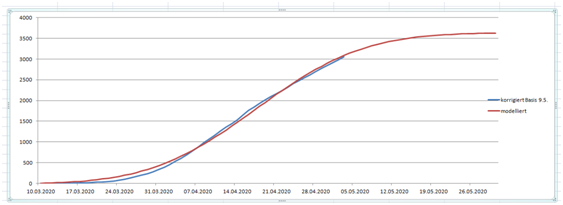
Update 7.5.20:
Kommen wir zur Endabrechnung, d.h. zur Verifikation oder Falsifikation des Modells!
Die Werte der täglichen Coronatoten in Schweden haben sich stabilisiert und ändern sich nicht mehr:
14.5.: 46
15.5.: 58
16.5.: 47
Wegen der 58 ist meine Prognose falsch, denn ich hatte <50 für Mitte Mai vorausgesagt.
Auch das Abklingen der Seuche unter 10 Todesfälle pro Tag wird einen Monat später eintreten als von mir vorhergesagt, also erst Ende Juni statt Ende Mai. Ich bin untröstlich!
Die Gesamtzahl der schwed. Opfer wird wohl gegen 6000 gehen und die Herdenimmunität erst bei 16% im Mittel eintreten.
Schweden hat seine Wirtschaft nicht ruiniert und in den großen Städten, also dort, wo in den nächsten Jahren die infizierten Touristen einschlagen werden, ist die erreichte Herdenimmunität noch viel höher. Das ist dann deren cordon sanitaire. Wir haben unsere Wirtschaft jetzt schon ruiniert und im Grunde keinerlei Immunität. Auch ein zweitesmal Stotterbremse kann ich mir nicht vorstellen. Aber da gibt es ja noch die Heilsversprechungen der Pharmaindustrie.
Die Prognosen der anderen (Wielers, Drosten, Merkel, WHO und der verbandelten Pharmaindustrie) lagen völlig daneben, selbst wenn man die Toten von den 52000 verschobenen Krebsoperationen in Deutschland auch noch auf das Konto von Corona anrechnet:
1,9 Millionen Virus-Tote in Deutschland? | The European
www.theeuropean.de › wolfram-weimer › 19-millionen...
09.03.2020 - Wie tödlich ist der Corona-Virus wirklich? ... Sollte die WHO-Zahl auf Deutschland zutreffen, würden hierzulande hunderttausende Tote drohen.
Hier noch eine abschließende Fage an hairbeRt zu seinem Kommentar vom 22 Apr: Soll ich mir "natürlich auch selbstehrlich genug eingestehen, dass ein Hausexperiment nicht die wissenschaftlich fundierte Meinung von Gesundheitsorganisationen wie der WHO widerlegen" kann?