Hallo,
Zeichne Dir so eine Treppenfunktion doch mal auf. Und markiere das Integral, d.h. die Fläche unter der Funktion:
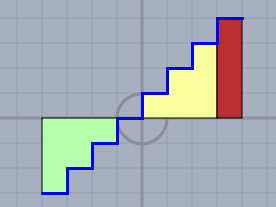
Die grüne Fläche zählt negativ, da sie sich im negativen Bereich befindet. Weiter ist die gelbe Fläche offensichtlich genauso groß wie die grüne, nur eben positiv. Da das Integral über die gesamte Fläche laufen soll und symmetrisch ist - also von \(-2\) bis \(+2\) heben sich die gelbe und grüne Fläche auf und es bleibt die rote Fläche stehen. Wenn diese \(=1\) sein soll, so wäre die abgebildete Funktion doch bereits eine Lösung, wenn die rote Fläche die Abmessungen \(0,5 \times 2\) hat - oder?
Nähern wir uns der Sache mal analytisch. Bei einer 'normalen' Treppe sind alle Stufen gleich tief und gleich hoch. Somit kann man doch schon annehmen, dass $$t_j - t_{j-1} = d \\ c_j = c_0 + h \cdot j$$wobei \(d\) die Stufentiefe und \(h\) die Höhe der Stufe ist. Weiter nehmen wir mal an, dass die Intregrationsgrenzen auch Stufengrenzen sind. Wir beginnen und enden also nicht mitten in einer Stufe. Dann setze ich das ein:$$\begin{aligned} \int_a^b f(x)\, \text dx &= \sum_{j=1}^n c_j(t_j - t_{j-1}) \\ &= \sum_{j=1}^n (c_0 + hj)d \\ &= d \sum_{j=1}^n c_0 \space + dh\sum_{j=1}^n j \\ &= dc_0 n + dh \frac n2(n+1) \\ &= dn\left( c_0 + \frac h2(n+1)\right)\end{aligned}$$Da von \(-2\) bis \(+2\) integriert werden soll, muss \(dn=+2-(-2)=4\) sein. Die anderen Parameter kannst Du jetzt frei wählen, um auf die gewünschte \(1\) zu kommen. Falls nichts anderes angegeben ist.
Für obige Skizze gilt: \(c_0 = -2\), \(n=8\) und \(h=0,5\).