Berechnen Sie die länge des Überhangs x.

Question

Aufgabe W 1

Als schiefster Turm der Welt gilt nach dem Guinness-Buch der Rekorde der Kirchturm im ostfriesischen Ort Suurhusen. Abb. 2 zeigt einen Längsschnitt des schiefen Turms. Die Zeichnung ist nicht maßstabsgerecht.

W 1.1 Der Winkel 5.2° gibt die Neigung der Turmmauer gegenüber der Senkrechten (Höhe h) an. Die Strecke \( x \) gibt den Überhang an (s. Abb. 2).

W 1.1.1 Berechne die Größe des Winkels \( \alpha \).
W 1.1 .2 Berechne die Länge des Überhanges \( x \). Runde auf Zentimeter.
W 1.2 Wegen Einsturzgefahr müssen an dem über 2000 Tonnen schweren Turm Sicherungsmaßnahmen durchgeführt werden. Eine Uberlegung ist, einen Eisenträger einzubauen (s. Abb. 2).
W 1.2 .1 Berechne die Länge \( t \) des Eisenträgers. Runde auf Zentimeter.

 

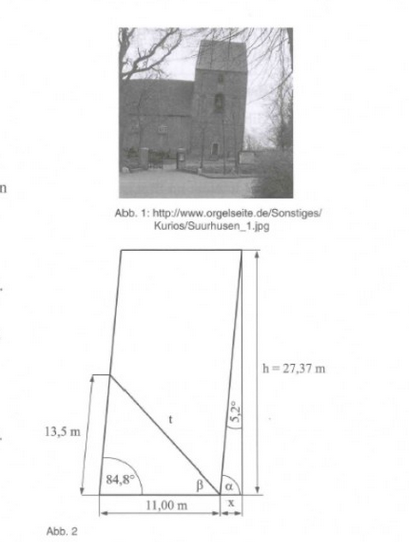
Aufgabe 1.1.2 und 1.2.1 weiß ich nicht, was ich machen soll.

Answer 1

Hallo,

zur Berechnung des Überhangs verwendest du den Tangens:

tan(α) = \( \frac{Gegenkathete}{Ankathetete} \)

tan(5,2) = \( \frac{x}{27,38} \)

Zur Berechnung von t verwendest du den Kosinussatz:

$$c^2 = a^2 + b^2 - 2·a·b·\cos(γ) \\ c = \sqrt{a^2 + b^2 - 2·a·b·\cos(84,8)}$$

a=13,5, b = 11

Comments

5.2 ist die neigung und α ist ja 84,8⁰

stimmt dann immernoch die rechnung

---

Ich habe den Winkel von 5,2° Grad auch alpha genannt, weil es zwei voneinander getrennte Rechnungen waren.

Answer 2

1.1.2) Definition des Tangens; x=27,37·tan(5,5°)

1.2.1) Kosinussatz; t²=11²+13,5²-2·11·13,5·cos(84,4)