Gebe für das obere Dreieck den fehlenden Innenwinkel an. Berechne die Länge der Katheten.

Question

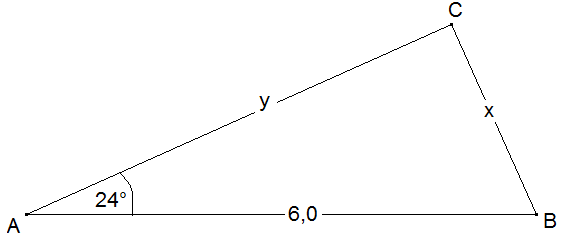
Ein Goldschmied stellt einen Schmuckanhänger aus zwei Platinbleche her der die nebenstehende Form aus zwei aneinander gefügten Dreiecken erhalten soll. Das obere Dreieck Ist rechtwinklig und hat eine Hypotenuse und der Länge 6,0 cm sowie den Innenwinkel Alpha=24 Grad.

Für das untere Dreieck wählt er die Seite AB um 1 cm länger als AC und die Seite BC wieder 1 cm länger als AB.

1 cm² des verwendeten Platinbleches wiegt 4,3 g.

a) Gebe für das obere Dreieck den fehlenden Innenwinkel an. Berechne die Länge der Katheten.

b) Ermittle rechnerisch den größten Innenwinkel des unteren Dreiecks.

c) Bestimme die Maße des Schmuckanhängers.

Skizze:

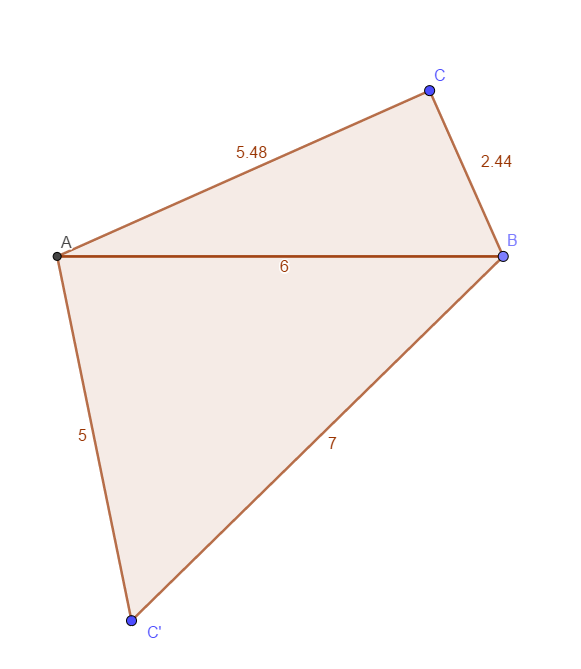
Das ist das untere Dreieck:

Comments

gebe für das obere Dreieck den fehlenden Innenwinkel an.

Warum tust du DAS nicht selbst?

Ein Innnenwinkel ist 90°, ein anderer Innenwinkel 24°.

Wie groß ist der dritte Innenwinkel?

---

Aufjedenfall ist das obere Dreieck rechtwinklig es schließt sich nach links. Darunter ist gleich das andere Dreieck und das schließt sich nach unten. Hoffe du weißt jz ungefähr wie es aussieht

Answer 1

a) x=6·sin(24°); y=6·cos(24°); β=90°-24°=66°

Comments

Wie kommst du auf 6•cos?

---

Nur dass wir deine Frage richtig deuten:

Bei

x=6·sin(24°)

fragst du NICHT nach, nur bei

y=6·cos(24°).

Heißt das also, dass dir x=6·sin(24°) klar ist?

---

Ja das ist mir klar

---

Dann weißt du also, dass im rechtwinkligen Dreieck der Sinus eines Winkels das Verhältnis aus GEGENkathete und Hypotenuse ist.

Ist euch eine vergleichbare Definition des Kosinus eines Winkels unterschlagen worden? Anders kann ich mir deine Unklarheit zum Kosinus nicht erklären.

Wie sieht eure Definition für den Kosinus eines Winkels aus?

---

Ich weiß bloß nicht wie du auf Kosinus kommst. Kann man das auch nur mit Sinus rechnen?

---

Das ist eine bemerkenswerte Antwort auf die konkrete Frage:

Wie sieht eure Definition für den Kosinus eines Winkels aus?