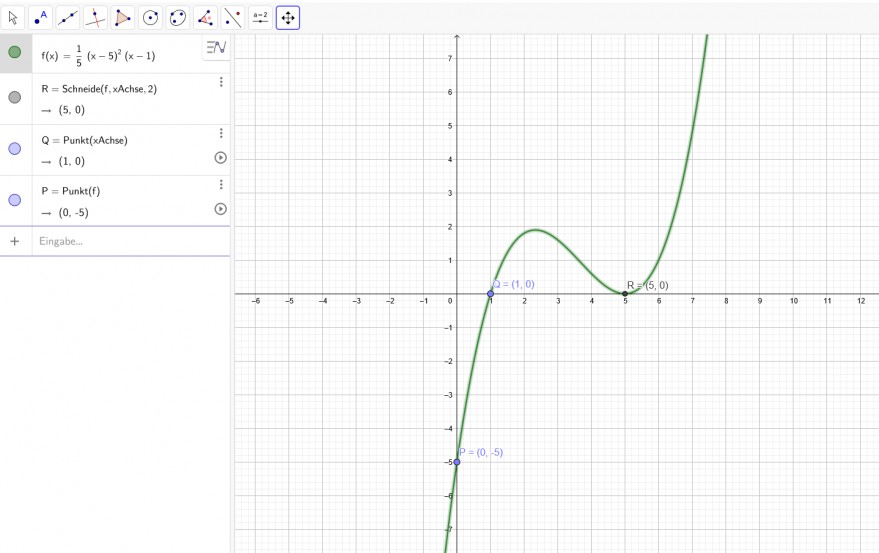
Der Graph einer ganzrationalen Funktion \( f 3 . \) Grades verläuft durch \( P\left(\frac{0}{-5}\right) \) und \( Q\left(\frac{1}{0}\right) \) und er berührt die \( x \) Achse im Punkt \( R\left(\frac{5}{0}\right) \)
\( f(x)=a(x-N 1) \cdot(x-N 2) \cdot(x-N 3) \)
x-Achse ist Tangente in \( R(5 \mid 0) \) -> doppelte Nullstelle und bei \( Q(1 \mid 0) \) eine einfache Nullstelle:
\( f(x)=a \cdot(x-5)^{2} \cdot(x-1) \)
\( P(0 \mid-5) \)
\( f(0)=a \cdot(0-5)^{2} \cdot(0-1)=-25 a \)
\( -25 a=-5 \)
\( a=\frac{1}{5} \)
\( f(x)=\frac{1}{5} \cdot(x-5)^{2} \cdot(x-1) \)