Ich habe mal den Grundaufbau der Kurvenuntersuchung unter folgendem Link dir aufgebaut: https://docs.google.com/document/d/1LFPdWAbmXw8BojJ2gKGyv1bG6yx1n1BjKYT-lBrSP8g/pub - Weggelassen habe ich die hinreichenden Bedingungen.
- - - -
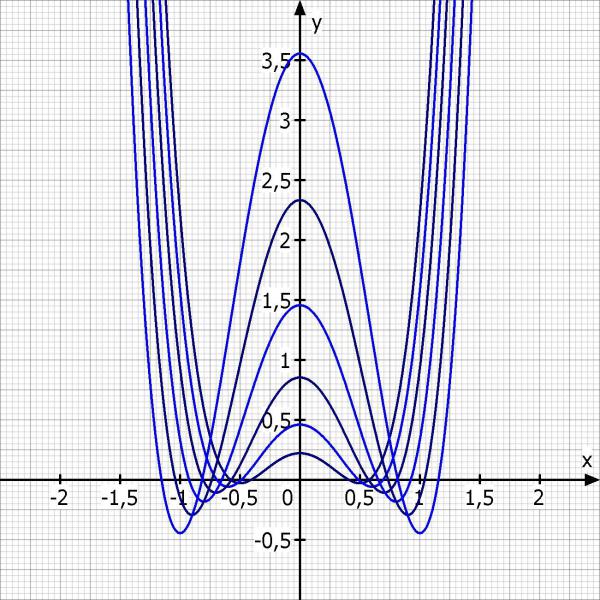
Kurvendiskussion: fk(x) = 4·x^4 - 2·k^2·x^2 + 2/9·k^4
Funktion und Ableitungen:
fk(x) = 4·x^4 - 2·k^2·x^2 + 2/9·k^4
fk'(x) = 16·x^3 - 4·k^2·x
fk''(x) = 48·x^2 - 4·k^2
Symmetrie
Achsensymmetrie zur Y-Achse weil alle Potenzen von x gerade sind.
Y-Achsenabschnitt f(0)
fk(0) = 4·0^4 - 2·k^2·0^2 + 2/9·k^4 = 2/9·k^4
Nullstellen fk(x) = 0
fk(x) = 4·x^4 - 2·k^2·x^2 + 2/9·k^4 = 2/9·(3·x^2 - k^2)·(6·x^2 - k^2)
3·x^2 - k^2 = 0
x = ± √3/3·k
6·x^2 - k^2 = 0
x = ± √6/6·k
Extremstellen fk'(x) = 0
16·x^3 - 4·k^2·x = 4·x·(4·x^2 - k^2) = 0
4·x = 0
x = 0
4·x^2 - k^2 = 0
x = ± k/2
fk(0) = 2/9·k^4 [Hochpunkt]
fk(± k/2) = - k^4/36 [Tiefpunkt]
Wendestellen fk''(x) = 0
48·x^2 - 4·k^2
x = ± √3/6·k
fk(± √3/6·k) = k^4/12 [Wendepunkt]
Skizze