Gleichung einer Parabel aufstellen

Question

Die Eisenbahnbrücke wird von einem Parabelbogen getragen der auf hängen mit 45 Grad Neigung steht 


wie lautet die Gleichung der Parabel 

Ich würde gerne ein Bild einfügen das geht aber nicht wen jemand die Aufgabe kennt ich brauche hilfeee

Comments

Vom Duplikat:

Titel: die eisenbahnbrücke wird von eimem parabelbogen getragen,der auf hängen mit 45 Grad Neigung steht...

Stichworte: rekonstruktion,sachaufgabe

:),

Ich komme bei einer Mathe Aufgabe nicht weiter...Die genaue Aufgabenstellung werde ich im Anhang hinzufügen,weil da eine Skizze abgebildet ist, die für die Aufgabe relevant ist.

Als Ansatz habe ich bis jetzt nur die allgemeine Funktionsformel der quadratischen Funktion aber ich komme nicht auf die 3 Bedingunen und bin momentan einfach richtig verwirrt :(

Wäre richtig cool,wenn mir jemand als Tipp einen Ansatz geben könnte :)

Aufgabe:

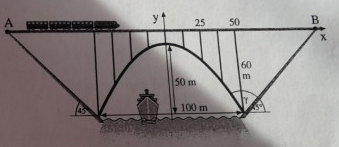
Die Eisenbahnbrücke wird von einem Parabelbogen getragen, der auf Hängen mit 45° Neigung steht.

a) Wie lautet die Gleichung der quadratischen Parabel?

b) Wie hoch sind die Brückenpfeiler, welche die Fahrbahn tragen?

c) Wie lang ist die Fahrbahn zwischen A und B?

d) Unter welchem Winkel α trifft der Brückenbogen die Böschungslinien?

---

Vom Duplikat:

Titel: Gleichung einer quadratischen Gleichung

Stichworte: parabel

Ich muss meine Hausaufgabe machen und ich kann eine Aufgabe nicht bearbeiten

Die Aufgabe lautet

Die Eisenbahnbrücke wird von einem Parabelbogen getragen, der auf Hängen mit 45 Grad Neigung steht

Wie lautet die Gleichung der quadratischen Parabel?

Das Bild meiner Aufgabe mit den Daten findet ihr hier : https://www.mathelounge.de/279988/eisenbahnbrucke-eimem-parabelbogen-getragen-hangen-neigung

Answer 1

Die Parabel, da sie mittig ist, hat die Funktionsgleichung

f ( x ) = a * x^2 + b

Gegeben
f ( 0 ) = a * 0^2 + b = 50 - 60 = -10
b = -10
f ( x ) = a * x^2 - 10
f ( 50 ) = a * 50^2 - 10 = 60

Helfe bei Bedarf gern noch weiter.

Comments

Danke für die schnelle Antwort erstmal :)

Ich verstehe aber deinen Ansatz nicht ganz..wie kommst du drauf dass a und b gleich null sind und wieso rechnest du 50- 60?...

---

Ich verstehe aber deinen Ansatz nicht ganz..wie kommst du drauf
dass a und b gleich null sind und wieso rechnest du 50- 60?...

Der höchste Punkt in der Mitte ist
( auf das Koordinatensystem bezogen )
-60 m Brückenhöhe + 50 m Parabelhöhe = -10 m
( 0 | -10 )

Für x = 0 gilt
f ( x ) = a * 0^2 + b = -10
b = -10

Korrektur
Fußpunkt ( 50 | -60 )
f ( 50 ) = a * 50² - 10 = -60

f ( x ) = -0.02 * x^2 - 10

Unten am Fußpunkt wäre die Steigung
f ´( x ) = -0.04 * x
f ´( 50 ) = -0.04 * 50 = -2
tan ( a ) = -2
a = -63.43 °

---

Hier der Graph

~plot~ -0.02 * x² - 10 ; [[ -50 | 50 | -60 | 0 ]] ~plot~

Answer 2

a) Wie lautet die Gleichung der quadratischen Parabel?

Nutze die Scheitelpunktform

f(x) = a * (x - Sx) + Sy

Kannst du sehen das der Scheitelpunkt bei (0 | -10) liegt? Dann hast du schon 2/3 der Form nur durch ablesen gemacht.

Jetzt gehen wir vom Scheitelpunkt Zum Bogenpunkt rechts unten auf der Böschung. Dazu müsstest du -50 in y-Richtung gehen und 50 in x-Richtung. Ist das klar?

Dann kannst du damit den Öffnungsfaktor a bestimmen

a = Δy / (Δx)² = -50/50² = -1/50 = -0.02

Das war das letzte Drittel. jetzt brauchen wir nur noch einsetzen und vereinfachen

f(x) = -0.02 * (x - 0) + (-10) = -0.02 * x - 10

Answer 3

Die allgemeine Funktion einer Parabel, die symmetrisch zur y-Achse ist, kann man so schreiben:

$$f(x)=ax^2+e$$

e ist dabei die y-Koordinate des Scheitelpunktes der Parabel. Wie du auf dem Bild siehst, ist der Scheitelpunkt 10 Einheiten unterhalb der x-Achse, also b = -10

$$f(x)=ax^2-10$$

Jetzt setzt du die Koordinaten eines Punktes in diese Gleichung ein, um a zu bestimmen. Man kann z.B. den Punkt P(50|-60) ablesen.

$$-60=a\cdot 50^2-10\\-50=2500a\\-\frac{1}{50}=a$$

Funktionsgleichung ist daher

$$f(x)=-\frac{1}{50}x^2 - 10$$

oder wie Georg es geschrieben hat

f ( x ) = -0.02x² - 10

ist das so verständlicher?

Comments

Aber es gibt doch noch ein Punkt der heist ( (-50/-60) was ist mit dem

---

Da die Punkte (50/-60) und (-50/-60) hier symmetrisch liegen braucht man nur einen davon benutzen. Welchen kannst du dir aussuchen.

---

Ob ich

$$-60=a\cdot 50^2-10\\$$

oder

$$-60=a\cdot (-50)^2-10$$

berechne, das Ergebnis ist das gleiche.

---

Dankeschön ich hätte da noch eine letzte frage ich versteh die Aufgabe b nich : wie hoch sind die Brückenpfeiler welche die Fahrbahn trägt ?

Wie berechnet man sowas

---

Der mittlere Pfeiler ist 10 m hoch, das ist klar, oder?

Er ist bei x = 0 und wenn wir null für x in die Funktionsgleichung einsetzen, ist das Ergebnis -10, also 10 m Höhe.

So bekommst du auch die anderen Längen: Den entsprechenden Wert für x in die Gleichung einsetzen und ausrechnen.