Question

Beweisen sie: Der Graph von f mit f(x)=x^2, die tangente an f in P(a/f(a) und die y-Achse begrenzen eine fläche mit dem inhalt A=1/3a^3

.Ich lerne gerade für eine Klausur und bin auf diese Aufgabe gestoßen und habe wirklich keinen Schimmer wie ich da vorgehen könnte..

Comments

Habe die Frage jetzt selber gelöst. Also hat sich erledigt;)

Answer 1

Betrachte folgende Skizze:

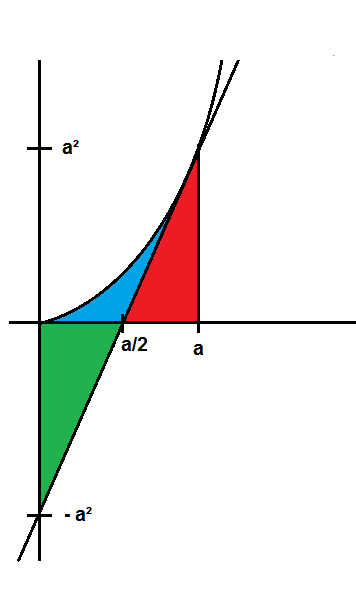
Die zu betrachtende Fläche ist blau und grün markiert.

Wenn es nun gelingt zu zeigen, dass der Inhalt der grünen Fläche gleich dem Inhalt der roten Fläche ist, dann ist klar, dass der Inhalt der blau-grünen Fläche gleich dem Inhalt der blau-roten Fläche ist. Der Inhalt der blau-roten Fläche aber ist gleich dem Integral von 0 bis a über x ² und dieser ist gleich ( 1 / 3 ) a ³.

Um zu zeigen dass der Inhalt der grünen Fläche gleich dem Inhalt der roten Fläche ist (beides sind rechtwinklige Dreiecke!) , genügt es zu zeigen, dass die Tangente an f ( x ) = x ² im Punkt ( a | f ( a ) = a ² ) ) die x-Achse an der Stelle a / 2 und die y-Achse an der Stelle - a ² schneidet, denn dann sind die Katheten der beiden Dreiecke jeweils a / 2 bzw. a ² Einheiten lang und somit beide Flächeninhalte gleich groß.

Also:

Die Tangente an f ( x ) = x ² hat an der Stelle a die Steigung m = f ' ( a ) = 2 a

Somit lautet ihre Gleichung in der Punkt-Steigungsform einer Geraden:

y = 2a ( x - a ) + a ²

<=> y = 2 a x - a ²

Die Tangente hat also den y-Achsenabschnitt - a ²

Setzt man y = 0 und löst nach x auf, erhält man den x-Achsenabschnitt:

0 = 2 a x - a ²

<=> a ² = 2 a x

<=> x = a ² / 2 a

<=> x = a / 2

Die Tangente hat also den x-Achsenabschnitt a / 2

Damit ist die Behauptung gezeigt. 

Comments

warum ist f(a)=a^2

---

Weil die Funktion f definiert ist als:

f ( x ) = x ² 

Damit ergibt sich für x = a :

f ( a ) = a ²