Hallo,
... und X,Y sowie P mal in Koordinaten dieser Basis zu beschreiben.
das brauchst Du gar nicht. Schau Dir folgende Skizze an:
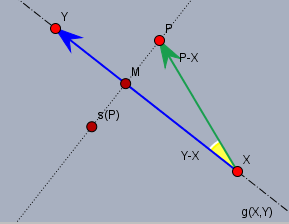
und vorher schreibe ich die 'Spiegelgleichung' noch etwas um $$s(P)=P+2\left(\frac{\langle Y-X | P-X\rangle}{\|Y-X\|^{2}}(Y-X)-(P-X)\right) $$und betrachten zunächst nur das innere Produkt (bzw. Skalarprodukt). Das multipliziere ich mit dem EInheitsvektor in Richtung \(Y-X\) und dividiere anschließend nochmal durch den Betrag \(|Y-X|\)$$\begin{aligned} \left< Y-X, \, P-X\right> &= |Y-X|\cdot |P-X| \cdot \cos(\alpha) \\ \left< Y-X, \, P-X\right> \cdot \frac{Y-X}{|Y-X|}&= |Y-X|\cdot |P-X| \cdot \cos(\alpha) \cdot \frac{Y-X}{|Y-X|} \\ \frac{ \left< Y-X, \, P-X\right>}{|Y-X|^2} (Y-X)&= \underbrace{|P-X| \cdot \cos(\alpha)}_{=|XM|} \cdot \frac{Y-X}{|Y-X|} \end{aligned}$$links steht nun der gleiche Term wie oben in der Gleichung und rechts steht doch der Vektor \(\vec{XM}\). Und es ist doch offensichtlich$$\vec{PM} = -(P-X) + \vec{XM}$$(siehe Skizze) und weiter muss gelten$$P' = P + 2 \vec{PM} = s(P)$$Frage bitte nach, falls etwas unklar ist.
Alternative Lösung:
\(s(P)\) liefert genau dann den Spiegelpunkt \(P'\), wenn \(s(P)P\) senkrecht zu \(Y-X\) steht und der Mittelpunkt \(M\) von \(s(P)P\) auf \(g(X,Y)\) liegt:$$\left< s(P) - P, Y-X \right> = 0 \\ \frac 12 (s(P) + P) - X = t (Y-X), \quad t \in \mathbb R$$