Aufgabe:
Gegeben seien zwei Geraden \( g, h \in \mathbb{G} \) mit \( g \| h \) und \( g \neq h \).
Zeigen Sie: Es gibt genau eine Gerade \( m \in \mathbb{G} \) mit \( S_{m}(g)=h \). Dabei gilt \( m \| g \) und \( m \| h \). Man nennt \( m \) Mittelparalelle von \( g \) und \( h \) und schreibt \( m_{g h}:=m \). Es handelt sich dabei um die (eindeutig bestimmte) Gerade, an der man \( g \) auf \( h \) spiegeln kann. Die Mittelparallele zweier (echt) parallel Geraden ist ebenfalls parallel zu diesen beiden Geraden.
Anleitung:
1.) Wählen Sie einen beliebigen Punkt \( A \in g \) und begründen Sie, dass die Lotgerade \( \ell \in \mathbb{G} \) zu \( g \) in \( A \) einen eindeutigen Schnittpunkt \( B \in \ell \cap h \) mit \( h \) besitzt.
2.) Betrachten Sie im Folgenden die (nach (GS2) eindeutige) Spiegelachse \( m_{A B} \in \mathbb{G} \) (siehe auch 5.13(b)) der Punkte \( A \) und \( B \).
Zeigen Sie zunächst, dass \( m_{A B} \| g \) und \( m_{A B} \| h \) gilt.
3.) Zeigen Sie schließlich für \( m \in \mathbb{G} \) die Äquivalenz: \( S_{m}(g)=h \Leftrightarrow m=m_{A B} \)
Für " \( \Leftarrow \) " begründen Sie (mit 4.9), dass \( S_{m}(g) \| g \) ist. Zudem ist \( B \in S_{m}(g) \) (wieso?). Nutzen Sie die Eindeutigkeit in (P).
Für " \( \Rightarrow \) " begründen Sie zunächst, dass \( m \| g \) sein muss (ein Widerpruchsbeweis hierzu ist möglich). Folgern Sie, dass \( A S_{m}(A) \perp g \) gilt und schließen Sie mit der Eindeutigkeit der Lotgeraden (5.7), dass \( S_{m}(A) \in \ell \) ist. Zudem ist \( S_{m}(A) \in h \) (wieso?).
Problem/Ansatz:
Ich habe die Aufgabe gelöst nur weiss ich nicht ob meine Lösung richtig ist. Ich muss morgen in meinem Tutorium die Lösung vorstellen deswegen wäre super lieb wenn jemand drüber schauen könnte ob die Lösung sinn ergibt :)
Vielen dank im voraus
Text erkannt:
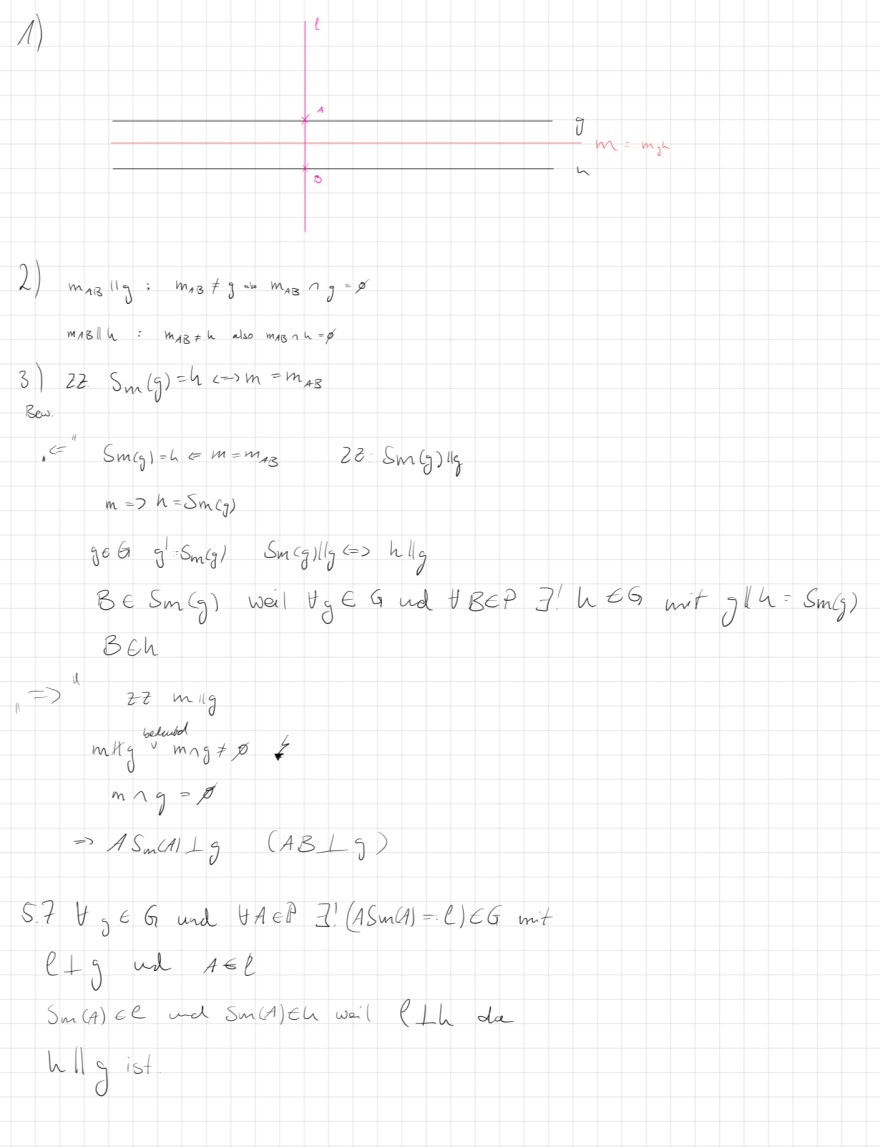
1)
2) \( m_{A B} \| g: m_{A B} \neq g \sim m_{A B} \cap g=\varnothing \)
\( m_{A B} \| h: m_{A B} \neq h \) also \( m_{A B} \cap h=\varnothing \)
3) \( 2 z \quad S_{m}(g)=h \Leftrightarrow m=m_{A B} \)
Bew.
\( \begin{aligned} \therefore & =\operatorname{Sm}(g)=h \Leftrightarrow m=m_{A B} \quad 2 z \cdot \operatorname{Sm}(g) \| g \\ & m \Rightarrow h=\operatorname{S} m(g) \end{aligned} \)
\( g \in G \quad g^{\prime}=S_{m}(g) \quad S_{m}(g) l g \Leftrightarrow h l_{g} \)
\( B \in \operatorname{Sm}(g) \) weil \( \forall g \in G \) nd \( \forall B \in P \quad \exists ! h \in G \) mit \( g \| h=S_{m}(g) \) Bch
\( \Rightarrow \quad z z \operatorname{mig} \)
\( \begin{array}{l} m * g \stackrel{\text { betuid }}{v} m \cap g \neq \varnothing \quad \xi \\ m \wedge g=\varnothing \\ \Rightarrow A S_{m}(A) \perp g \quad(A B \perp g) \end{array} \)
\( 5.7 \forall g \in G \) und \( \forall A \in \mathbb{P} \exists^{\prime}(A \sin (A)=l) \in G \) mit
\( l+g \) an \( A \in l \)
\( \operatorname{Sm}(A) \in e \) and \( \sin (A) \in h \) wail \( l \) Lh da hllg ist