Aufgabe:
Im Rechteck mit den Seitenlängen a = 2 und b = 3 wird von P1 über P \( _{2} \), P\(_{3}\) usw. ein Streckenzug mit unendlich vielen Strecken gezeichnet. Die grauen Dreiecke werden der Reihe nach nummeriert (vgl. Abbildung)
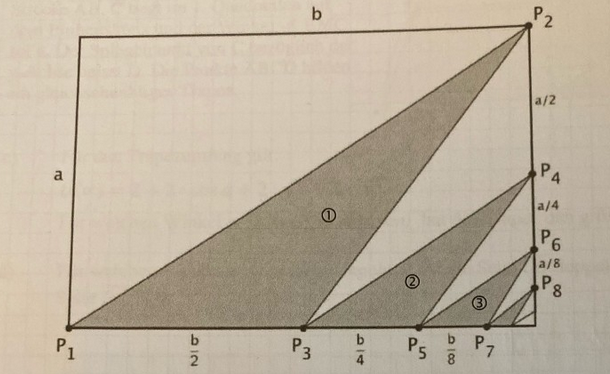
a) Berechnen Sie die Summe der Umfänge aller (unendlich vielen) grauen Dreiecke.
b) Wie viel Prozent der Rechtecksfläche wird von den (unendlich vielen) grauen Dreiecken abgedeckt?
c) Welche Nummer trägt das erste Dreieck mit Flächeninhalt kleiner als \( 10^{-4} \) ?
d) Der Zickzack-Weg \(P_1, P_2,P_3,P_4,P_5,....\) wird immer länger. Wie viele Wegstücke muss man mindestens summieren, damit der Weg eine Länge von mehr als 12 erhält?
Moin servus
Wie kann ich alle diese Aufgaben machen? Wie komme ich bei a) auf die methode zum die Summe aller unendlich vielen Dreiecken zu berechnen?? Hat das was mit dem thema „Folgen und Reihen“ zu tun?
Bei b): wenn ich a) hätte, habe ich ja die UMFÄNGE und nicht den FLÄCHENINHALT, wie soll man denn da auf die Fläche kommen??
Bei c): Müsste ich da einfach knobeln? (wenn ich b) hätte würde ich es vielleicht verstehen)
Bei d) da habe ich garkeine ahnung was machen