Hallo. Ich brauche Hilfe bei folgender Aufgabe. Ich hab die Matrix zwar aufgestellt aber es würde mir nicht gelingen an einer Stelle etwas zu eliminieren ohne das wo anders wieder etwas Neues auftaucht. Wie gehe ich mit diesem Problem um ?
Aufgabe:
(a) Von einem Arithmogon sind lediglich die Zahlen in den Rechtecken bekannt:
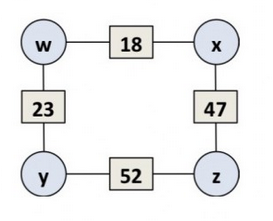
Ermitteln Sie alle Möglichkeiten für die Eckzahlen \( w, x, y \) und \( z \)
(b) Wir betrachten nun den allgemeinen Fall: Von einem Arithmogon sind nur die Zahlen \( a, b, c \) und \( d \) in den Rechtecken bekannt (diese Zahlen müssen nicht notwendigerweise voneinander verschieden sein), während man nichts näheres über die Eckzahlen weiß.
Stellen Sie das zugehörige lineare Gleichungssystem auf und ermitteln Sie, in welchem Fall es keine Lösung, genau eine Lösung bzw. unendlich viele Lösungen gibt. Geben Sie jeweils die Lösungsmenge explizit an.