Aufgabe:
Wir betrachten eine Funktion \( f(x)=a \sin (b x+c)+d \) für reelle Zahlen \( a, b, c, d \) mit \( a, b \neq 0 . \) Die Periodenlänge \( T \) von \( f \) ist definiert als die kleinste reelle Zahl \( T>0, \) sodass \( f(x+T)=f(x) \) für alle \( x \in \mathbb{R} \) gilt. Die Amplitude \( A \) von \( f \) (auch maximale Auslenkung genannt) ist die Höhe der Maxima über der horizontalen Symmetrieachse des Graphen.
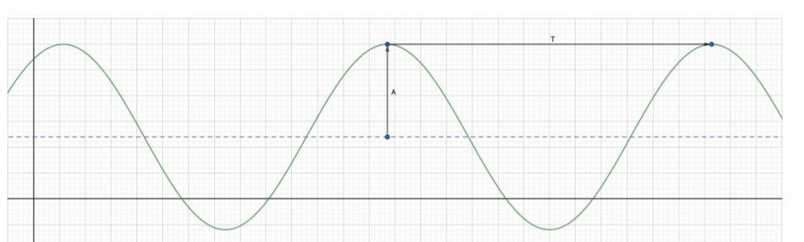
Abbildung 1: Graph von \( f \) mit eingezeichneter Periodenlänge \( T \) und Amplitude \( A \)
a) Bestimmen Sie \( T \) und \( A \) für \( f(x)=4 \sin \left(\frac{\pi}{2} x\right)+6 \)
b) Wie kann man \( T \) und \( A \) allgemein aus \( a, b, c, d \) berechnen?
c) Bestimmen Sie Zahlen \( a, b, c, d \) so, dass die dazugehörige Funktion \( f \) Periodenlänge \( \pi \) und Amplitude 2 hat und bei 0 das Maximum \( f(0)=3 \) annimmt.
(Die Zahl \( c \) ist nicht eindeutig bestimmt, es genügt eine mögliche Lösung anzugeben.)
Bei a) habe ich für T: p = \( \frac{2π}{\frac{π}{2}} \) = 4π und für A= 4 (war gegeben). War das jetzt schon alles der muss ich da mehr machen ?
Und wie gehe in den anderen Aufgaben vor ?
