Hallo Moni,
(a) senkrecht zur x-y-Ebene des Koordinatensystems
diese Variante kann man ausschließen, da die Ebene durch \(ABC\) senkrecht auf der XY-Ebene steht. Befände sich \(S\) senkrecht zur XY-Ebene oberhalb von \(A\), dann wäre die Pyramide so flach, dass sie ein Volumen von 0 hätte.
Also können wir wohl davon ausgehen, dass der Vektor \(\vec{AS}\) senkrecht auf der Ebene durch \(ABC\) steht. Um diesen Vektor zu berechnen bildet man zunächst das Kreuzprodukt aus \(\vec{AB} \times \vec{AC}\)$$\begin{aligned} \vec{AB} &= \vec B - \vec A = \begin{pmatrix}4\\ 3\\ 2\end{pmatrix} - \begin{pmatrix}1\\ 0\\ -1\end{pmatrix} = \begin{pmatrix}3\\ 3\\ 3\end{pmatrix} \\ \vec {AC} &= \vec C - \vec A = \begin{pmatrix}-2\\ -3\\ 5\end{pmatrix} - \begin{pmatrix}1\\ 0\\ -1\end{pmatrix} = \begin{pmatrix}-3\\ -3\\ 6\end{pmatrix} \\ \vec{AB} \times \vec{AC} &= \begin{pmatrix}3\\ 3\\ 3\end{pmatrix} \times \begin{pmatrix}-3\\ -3\\ 6\end{pmatrix} = \begin{pmatrix}27\\ -27\\ 0\end{pmatrix}\end{aligned}$$Dieser Vektor, hat die Länge $$\sqrt{27^2 + (-27)^2 + 0^2} = 27 \sqrt 2$$Wir benötigen aber einen Vektor mit der Länge \(5 \sqrt 2\) also skalieren wir ihn mit \(5/27\)$$\vec{AS} = \begin{pmatrix}27\\ -27\\ 0\end{pmatrix} \cdot \frac {5}{27} = \begin{pmatrix}5\\ -5\\ 0\end{pmatrix}, \quad |\vec{AS}| = \sqrt{5^2 + (-5)^2 + 0^2} = 5 \sqrt 2$$und der Punkt \(S\) liegt dann bei $$\vec S = \vec A + \vec{AS} = \begin{pmatrix}1\\ 0\\ -1\end{pmatrix} + \begin{pmatrix}5\\ -5\\ 0\end{pmatrix} = \begin{pmatrix}6\\ -5\\ -1\end{pmatrix}$$Zur Illustration noch ein Szene im Geoknecht3D
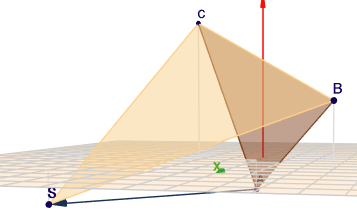
(klick auf das Bild, dann öffnet sich die Szene im Geoknecht3D)
Man kann den Vektor \(\vec{AS}\) auch negieren, dann läge \(S\) auf der anderen Seite der Grundfläche. Das wäre genauso eine Lösung. Nur der Umlaufsinn des Dreiecks \(\triangle ABC\) wäre bezogen auf die Höhe negativ.
Gruß Werner