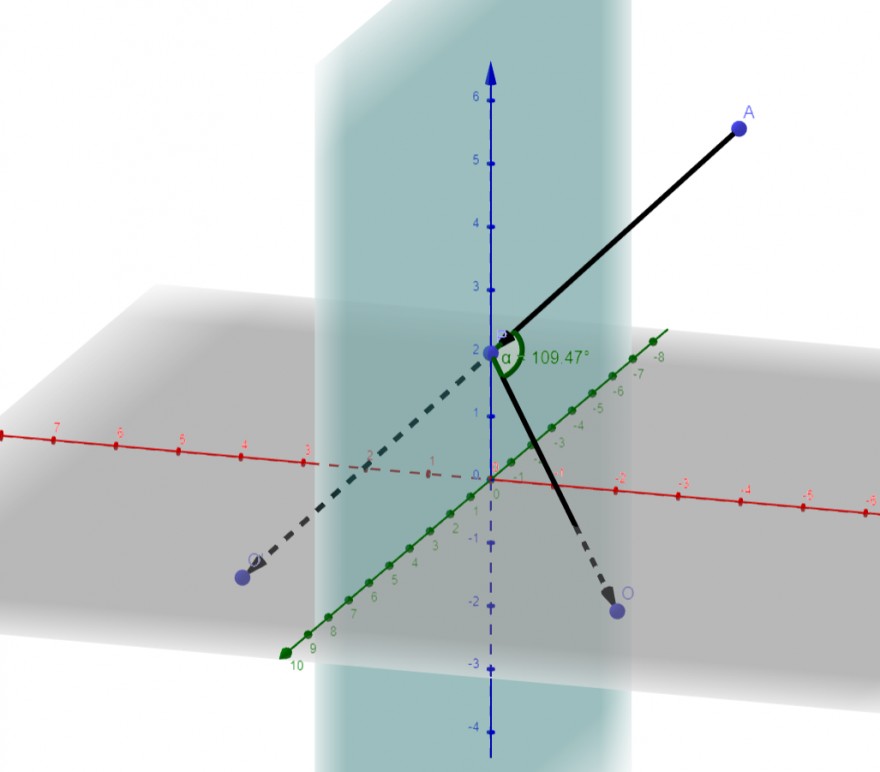
a) In welche Richtung schaut das Auge um das Objekt im Spiegel zu sehen?
[3, 3, -1] - [-3, -3, 5] = [6, 6, -6] = 6·[1, 1, -1]
b) In welchem Punkt P auf dem Spiegel sieht man das Objekt?
[-3, -3, 5] + 3·[1, 1, -1] = [0, 0, 2]
c) Wie groß ist der Winkel OPA?
[1, 1, -1] * [1, 0, 0]
2·ARCCOS([1, 1, -1]·[1, 0, 0]/(ABS([1, 1, -1])·ABS([1, 0, 0]))) = 109.5°