Nullstelle von \(f(x)=x^4-2x^2\) Hier klappt es mit ausklammern von \(x^2\)
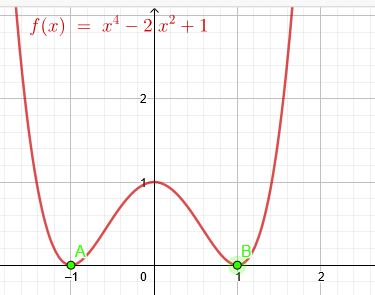
Anders ist es nun bei \(p(x)=x^4-2x^2+1\)
Hier kann man mit \(x^2=z\) substituieren oder aber folgenden Weg beschreiten
\(p´(x)=4x^3-4x\)
\(4x^3-4x=0\) → \(x^3-x=0\) → \(x(x^2-1)=0\)
Extremwert bei:
\(x_1=0\) \(p(0)=1\) demnach liegt keine Nullstelle vor
\(x^2-1=0\)
\(x_2=1\) \(p(1)=1-2+1=0\) ist wegen Extremwert eine doppelte Nullstelle
\(x_3=-1\) \(p(-1)=(-1)^4-2\cdot (-1)^2+1=0\) ist auch wegen Extremwert eine doppelte Nullstelle.
Somit existieren 4 Nullstellen.