Question

Mechanischer Oszillator: gedämpfte und ungedämpfte Schwingungen:

Die Abbildung zeigt das t-s-Diagramm der gedämpften Schwingung eines mechanischen Oszillators der Masse \( \mathrm{m}=380 \mathrm{g} \)

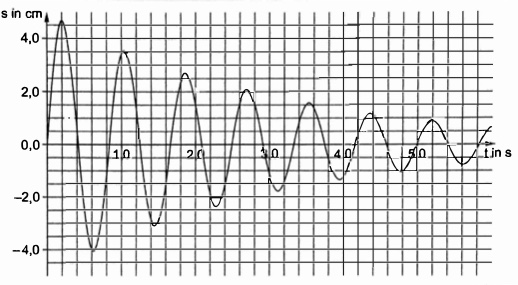
1. Ermitteln Sie die Frequenz f des gedämpften Oszillators.

2. Bestimmen Sie die Änderungsrate a der Amplitude des Oszillators während einer Periode T aus den ersten sechs Amplituden in Abbildung 1.

3. Zeichnen Sie den Aufbau eines ungedämpften und eines gedämpften Oszillators und erklären Sie den Unterschied.

4. Vergleichen Sie, wie sich die mechanische Gesamtenergie beim gedämpften und beim ungedämpften mechanischen Oszillator während der ersten 5 s der Schwingung verhält.

5. Lesen Sie in Abbildung 1 die Elongation (Auslenkung) \( s_{1} \) und \( s_{2} \) des gedämpften Oszillators zu den Zeitpunkten \( t_{1}=1,04 \) s und \( t_{2}=1,86 \) s ab und ermitteln Sie die mechanischen Gesamtenergien in \( \mathrm{t}_{1} \) und \( \mathrm{t}_{2} \)

6. Schätzen Sie die mechanische Gesamtenergie des gedämpften Oszillators zur Zeit \( t_{3}=1,6 \mathrm{s} \) ab.

7. Berechnen Sie, ab welcher Periode die Amplitude des gedämpften Oszillators kleiner als \( 10 \% \) seiner ursprünglichen Amplitude ist.

Answer 1

Hallo

 1. sieht so aus, als sei Die Schwingungsdauer 10,2s daraus f.

2. ist ja nur ablesen  und  von 6T auf 1T schließen

3. kannst du hoffentlich

jetzt kommt es drauf an, wie genau ihr die mechanische Schwingung bei einer Feder bestimmt habt, kennst du den Zusammenhang zwischen Frequenz, masse und Federkonstante? dann bestimme die Federkonstante, und die Geschwindigkeiten an den gefragten Punkten,

am besten fängst du damit an, dir die Gleichung der gedämpften Schwingung aufzuschreiben, und dann an den Stellen zu fragen, wo du nicht weiter weisst.

Gruß lul