Aufgabe:
In der letzten Woche hast du gelernt, wie du den Flächeninhalt unter einem Graphen berechnest und was dieser im Zusammenhang bedeutet.
Hier siehst du den Graphen der Zu- und Abflussrate eines Wasserreservoirs. Durch einen Kanal kann dieses mit Wasser gefüllt und durch einen zweiten Kanal entleert werden. Zu Beginn (t=0) befinden \( \operatorname{sich} 600 m^{3} \) Wasser im Reservoir.
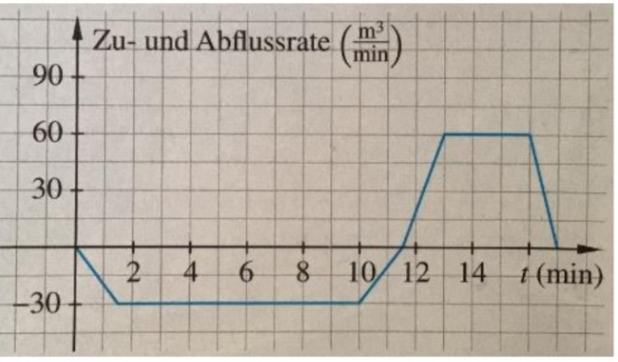
Aufgaben
a) Beschreibe, wie sich der Wasserstand zwischen \( t=0 \) und \( t=17 \) ändert.
b) Auf der x-Achse ist die Zeit in Minuten (min) angegeben. Auf der y-Achse ist die Rate in Kubikmeter pro Minute \( \left(\frac{m^{3}}{m i n}\right) \) angegeben. Gib die Einheit an, welche du für den Flächeninhalt unter dem Graphen in diesem Sachzusammenhang benutzt. Erläutere den Zusammenhang zwischen den beiden Einheiten der Achsen und der Einheit des Flächeninhalts.
c) Berechne die Füllmenge des Reservoirs zu folgenden Zeiten. Teile dazu zunächst die Flächen unter dem Graphen in einzelne Teilflächen ein, die du leicht berechnen kannst.

d) Erstelle ein Koordinatensystem und zeichne den Graphen ein, der die Füllmenge des Reservoirs in Abhängigkeit von der Zeit darstellt.