Der vorliegende fiktive Datensatz enthält Daten von 200 Jeans-Bestellungen eines Großhändlers für Jeans in Deutschland. Die Variablen im Datensatz sind: der Preis [in Dollar pro Packungseinheit] (preis), die bestellte Menge [Anzahl der Packungseinheiten] (menge) und die Qualität der Jeans. Bei der Qualität wird unterschieden, ob es sich bei den Jeans um no-name Produkte (noname), Markenprodukte (marke) oder Designer-Jeans (designer) handelt. Eine lineare Regression mit dem Preis als abhängige Variable und der Menge sowie der Qualität als unabhängige Variablen liefert den folgenden R-Output, wobei die Qualität durch Dummyvariablen ersetzt wurde. Die Dummyvariable noname nimmt den Wert 1 an, wenn es sich um no-name Jeans handelt, ansonsten den Wert 0. Analog gilt dies für die Dummyvariable marke.
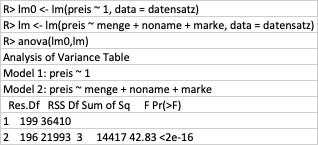
R> lm0 <- lm(preis ~ 1, data = datensatz)
R> lm <- lm(preis ~ menge + noname + marke, data = datensatz)
R> anova(lm0,lm)
Analysis of Variance Table
Model 1: preis ~ 1
Model 2: preis ~ menge + noname + marke
Res.Df RSS Df Sum of Sq F Pr(>F)
1 199 36410
2 196 21993 3 14417 42.83 <2e-16
Text erkannt:
\( \mathrm{R}>\operatorname{lm} 0<-\operatorname{lm}(\text { preis } \sim 1, \text { data }=\text { datensat } 2) \)
\( \mathrm{R}>\operatorname{lm}<-\operatorname{lm}(\text { preis } \sim \text { menge }+\text { noname }+\text { marke, data }=\text { datensatz }) \) \( \mathrm{R}> \) anova \( (\mathrm{lm} \mathrm{O}, \mathrm{Im}) \)
Analysis of Variance Table Model 1: preis \( ^{\sim 1} \) Model 2: preis \( ^{\sim} \) menge \( + \) noname \( + \) marke Res.Df RSS Df Sum of Sq \( F P r(>F) \)
119936410
\( 2 \quad 196219933 \quad 1441742.83<2 e-16 \)
Bestimmen Sie das Bestimmtheitsmaß (R²) in %.